Dit is een door mij geschreven hoofdstuk uit het boek De onvermijdelijke culturele revolutie / |red. H. Konstapel, E. Vreedenburgh, G.J.P. Rijntjes, SMO 1998.
Dit artikel trekt lering uit de ervaringen die ik heb opgedaan met het besturen van softwarecomplexen.
Onder besturen versta ík dat er iemand is, die weloverwogen, op basis van kennis van zaken, sturing geeft aan een proces van ontwikkeling. Onder een softwarecomplex versta ik een grote hoeveelheid geautomatiseerde code die zeer complex is opgebouwd.
In het algemeen is dit het geval als software ouder wordt. Er is dan niemand meer, die bij het origineel betrokken is geweest en de documentatie is weg of verouderd.
Een andere complicerende factor is gekochte software, zoals WINDOWS. De nieuwe eigenaar heeft er geen idee van hoe deze software werkt. Op dit ogenblik zit al meer dan 95% van de software “onder de motorkap” in de PC.
De afhankelijkheid van deze software is bij veel gebruikers erg groot. We zijn de gevangenen geworden van de ons omringende software.
Met een beschrijving van mijn eigen ontwikkelingsgang, wil ik in vogelvlucht de ontwikkelingen in de automatisering en de besturing van automatiseringsprocessen tussen 1970 en nu in kaart brengen.
Er toont zich in die periode een exploderende diversiteit aan software en ondanks verwoede pogingen een steeds verder afnemende besturing door het individu. Op dit moment is er zelfs geen sprake meer van besturing van processen maar van autonome groei.
Vervolgens beschrijf ik gedrag van mensen in relatie tot complexe situaties en zal laten zien, dat we op dit punt niet sterk staan. Mensen zijn overlevingsmachines en geen analisten.
Daarna pak ik de evolutie-theorie op. Deze theorie lijkt bruikbaar om op termijn, nieuwe wijzen van besturen van de ontwikkeling van het softwarecomplexen te ontdekken.
Als laatste probeer ik alle vergaarde kennis te gebruiken om te laten zien hoe besturen mogelijk is door te spelen met tussenschotten, lagen en stromen.
Programmeren
Mijn eerste ervaringen met computers en computertalen deed ik op in de periode 1969 – 1980. In deze periode studeerde ik wiskunde in Leiden en deed mijn eerste werkervaring op als Operations Research Analist bij de Algemene Bank Nederland (ABN).
Deze eerste ontwikkelingsfase is te typeren met de term programmeren. Er werd veel aandacht geschonken aan het maken van programma’s en nog weinig aan ontwerpen of besturen. Dit was ook niet nodig, omdat er niet veel ontwikkelaars en programma’s waren.
Ik zag mijn eerste computer of beter een stukje van de computer, de kaartlezer, in 1969 in het Centraal Rekeninstituut van de Universiteit Leiden. Hij stond in de hal en mensen met dozen vol ponskaarten omringden hem. Het duurde een dag, voordat je zeker wist, dat alles wat je op die kaarten had ingetikt ook zonder tikfouten was. Dat betekende echter nog niet, dat het programma realiseerde wat je er van verwachtte.
Studenten Wiskunde werden getraind in ALGOL en Assembler. De laatste taal was een machinetaal gericht op computers van IBM. Assembler was het summum van onbegrijpelijkheid. Je verschoof steeds kleine stukjes data in binaire vorm van het ene geheugenplekje naar het andere plekje.
ALGOL, de moeder van alle computertalen, was bedacht om deze narigheid onzichtbaar te maken. Door een ander programma werd ALGOL omgezet in Assembler. Weer een ander programma zette Assembler om in nullen en enen (de machinecode).
Het laten werken van programma’s gaf een enorme kick. Na soms weken puzzelen en erg veel wachten op output deed hij het.
Naast de praktijk van het programmeren kregen we ook theorie over talen (Chomsky), machines (Turing) en programmeren (Dijkstra).
Langzamerhand werd duidelijk, dat we iets in handen hadden, dat de wereld zou veranderen. Het werd duidelijk dat met de computer of beter gezegd met de computertaal ideeën supersnel om te zetten zijn in acties.
Computertalen
De denkbeelden van Chomsky hebben grote invloed uitgeoefend op de computertalen. Door het combineren van woorden en patronen (de syntax) ontstaan oneindig veel mogelijkheden.
Het omgekeerde, het vinden van woorden en patronen in de resultaten, kreeg mijn aandacht. Was het mogelijk om hier een methode voor te bedenken? Het vertalen van de ene naar de andere taal leek een kwestie van tijd te zijn. Maar tot op heden zijn we in beide gebieden nog aan het speuren naar de ultieme oplossingen.
Door veel te lezen over de geschiedenis van de filosofie (Störig, Russell) ontdekte ik, dat taal en vertalen de mens al eeuwen hebben beziggehouden.
In bijvoorbeeld de Culturele Antropologie (Levi-Strauss) wordt geprobeerd om de woorden en de patronen te vinden in culturen.
Chomsky en Turing hebben laten zien, dat er een groot verschil is tussen computertalen en mensentalen. Bij een computertaal is de betekenis (semantiek) eenduidig en kunnen woorden vertaald worden door ze stuk voor stuk te lezen en te interpreteren. Er bestaat geen twijfel over wat er moet gebeuren.
In een mensentaal moet je soms “heen-en-weer” in de tekst om de juiste betekenis te vinden. Er is hierbij sprake van contextgevoeligheid.
Ook is de plaats van een woord ten opzichte van een ander woord belangrijk voor de betekenis ervan. Bovendien kunnen dezelfde woorden verschillende betekenissen hebben.
Het verschil tussen computer- en mensentalen heeft een enorme invloed gehad op de automatisering. Steeds heeft men geprobeerd om de structuur van de computertaal aan de gebruiker op te dringen omdat dit niet lukte werd de automatisering/software steeds complexer.
De computer beschikt slechts over een beperkt aantal woorden en patronen. Hoe dichter je de computer nadert, met als minimale taal de machine code, hoe minder woorden en patronen er zijn.
De variatie in (output-)mogelijkheden neemt hierdoor toe. Iedere ontwikkelaar van een nieuwe computertaal maakt, meestal impliciet, een keuze voor het makkelijk bereiken van een bepaald soort eindresultaat, met veel vaste woorden en patronen, of voor veel variatie in dit resultaat.
Technici houden van talen die dicht bij de computer staan. Eindgebruikers willen het omgekeerde: een taal die het meest lijkt op een mensentaal.
Zo zijn er in de loop der tijd steeds nieuwe talen ontstaan, die naast elkaar staan of op elkaar zijn gebaseerd. Zo wordt een taal soms via een laag van vertalers naar de computer gebracht. Dit vertalen kost allemaal tijd.
Hoe meer de taal kan hoe langer het duurt voordat het resultaat zichtbaar wordt. Door de steeds maar weer toenemende kracht van de computer valt het niet op dat er zeer veel werk wordt verstouwd.
Aan de ontwikkelde computertalen zijn generaties toegekend, die worden aangeduid met nummers (1e Generation Languages 1GL). De ontwikkeling van machinecode (1e generatie) via Assembler (2e generatie) naar Algol (3e generatie) lijkt te zijn geëindigd in de 4de generatie ( SQL).
Het ontwikkelen van de 5de generatie taal (Artificial Intelligence) is ondanks hoge investeringen tot op heden niet gelukt.
Computers werken niet exact
Het leukste vak tijdens mijn studie vond ik Numerieke Wiskunde. Complexe wiskundige structuren werden afgebroken in door de computer te gebruiken bouwstenen.
Zo is machtsverheffen niets anders dan een aantal keren vermenigvuldigen en zijn sinus en cosinus reeksontwikkelingen.
Veel mensen weten niet dat het meestal niet mogelijk is om een berekening exact door een computer te laten uitvoeren. Men probeert dan een benadering te vinden.
Het toepassen van benaderingen op benaderingen maakt, dat de afrondfout steeds groter wordt. Zoals gesteld zijn de meeste computergebruikers zijn zich hiervan niet bewust.De computer wordt gezien als het wonder van exactheid.
Het aan elkaar verbinden van een groot aantal benaderde berekeningen, zoals in een groot wiskundig model geeft uiteindelijk een onvoorspelbaar resultaat dat tussen grote marges van onzekerheid ligt.
De meeste onderzoekers kunnen deze marge niet tonen of willen hem niet tonen. Ze geven liever hun eindresultaat in de vorm van een getal met het liefst vele cijfers na de komma.
Leren
Als bijvak voor mijn doctoraal deed ik Onderwijskunde. Het meest interessante gedeelte was voor mij Leerpsychologie.
Gagné beschreef leren als een gradueel proces, waarbij lagere structuren, zoals stimulus en respons, zich opbouwden tot het summum van de “problem-solving”. De theorie van Gagné geeft een indeling, maar verklaart weinig.
Piaget (The psychologie of intelligence, 1986) ontwikkelde een theorie die gebaseerd is op “sprongsgewijs” leren.Mensen leren door gegevens en ervaringen op te slaan in bestaande mentale vormen (assimilatie) of door het herstructureren van deze structuren (accommodatie). Dit laatste gaat gepaard met allerlei vaak ook emotionele bijeffecten (ziekte, stress).
Accommodatie grijpt veel dieper in op de mens dan enkel op mentaal niveau. Het kan bijvoorbeeld het immuunsysteem aantasten. Deze bevindingen zag ik terug in mijn latere werkzaamheden als leidinggevende van een ontwikkelafdeling en als betrokkene bij grote veranderingsprojecten.
Echte problemen zijn onoplosbaar
Na mijn afstuderen in 1976 kwam ik in dienst van ABN op de afdeling Operations Research. Hier was men, dacht ik, bezig om “het grote exacte werk” te verrichten. De afdeling bestond uit econometristen en wiskundige ingenieurs.
Ik was, naast mijn baas de enige echte Drs. Wiskunde. Al snel ontdekte ik, dat echte automatiseringsproblemen onoplosbaar waren en je ergens moest gaan “sjoemelen” om met een oplossing te komen.
Een mooi voorbeeld is het optimaliseren van databasestructuren. Na het bestuderen van boeken en gesprekken met databaseontwerpers ontdekten we, dat er vele optimalisatie manieren waren, die ieder als dé manier werden bestempeld.
Een wiskundige analyse van het probleem liet zien, dat het vrijwel onmogelijk was om in redelijke tijd een oplossing te vinden voor het optimaliseren van database-structuren.
Hierbij kwam het probleem, dat een kleine verandering van de waarden (bijvoorbeeld het aantal banktransacties per dag) aanleiding gaf tot grote veranderingen in de oorspronkelijke structuur.
Toch bleken de database-ontwerpers niet te overtuigen van de in essentie onoplosbaarheid van deze automatiseringsproblemen. Net als bij andere existentiële vraagstukken bleek de het onoplosbare karakter ervan te leiden tot het aanhangen van een geloof.
APL en de druk om te verwezenlijken.
APL, “A Programming Language”, is een taal gemaakt voor wiskundigen. Oorspronkelijk was ze bedoeld als instrument om wiskunde onderwijs te geven. APL slaat alle gegevens op in matrices. Deze manier van opslaan is uitermate flexibel en liep ver vooruit op latere ontwikkelingen zoals de relationele database.
Met APL worden alle bewerkingen direct in het geheugen uitgevoerd. Men noemt dit een interpretor. Het directe werken met de hardware gaat ten koste van de uitvoeringssnelheid.
Talen, die in onderliggende talen worden vertaald bieden de mogelijkheid om te worden geoptimaliseerd. In het algemeen kan men dan kiezen voor optimalisatie van het ruimtegebruik of van de verwerkingssnelheid.
APL is de meest perfecte “direct link” tussen (wiskundige) hersenen en de computer. Na een langdurige inleerperiode was de programmeur in staat om de meest complexe problemen in een paar symbolen te vangen.
Er werd ook een sport van gemaakt om programma’s steeds compacter te maken. Na deze inkrimping van het aantal symbolen snapte niemand meer wat het programma beoogde, behalve de ontwikkelaar. Maar na enige tijd wist deze het ook niet meer. Pas na een langdurige studie kon de ene programmeur het onderhoud van de programma’s van een ander overnemen.
Er werd om dit probleem te voorkomen aangedrongen op het maken van documentatie in het programma of daar buiten. Door de programmeurs werd dit gezien als tijdverspilling.
Er bestond een enorme druk om steeds maar weer nieuwe ideeën te verwezenlijken. Een goede administratieve afwerking leverde geen punten op.
Na enige tijd werd ik betrokken bij het maken van delen van wiskundige modellen. Deze modellen hadden tot doel om de ontwikkeling van de rente te voorspellen op basis van tijdreeksen. Hiertoe werd een complete prognosefabriek gebouwd in APL, die met behulp van een modelgenerator (Box-Jenkins)* een grafische terminal van Tectronix* aanstuurde.
Per maand werd volautomatisch een doos met plotjes met grafieken afgeleverd en aangeboden aan de bedrijfseconomen. Het viel mij op, dat men geen aandacht schonk aan afrondfouten, die APL veroorzaakte.
Er werden door APL namelijk zeer complexe programma’s aan elkaar geknoopt. Daarnaast werd ook de statistische fout niet getoond. De klant kreeg prachtige grafieken en had een groot vertrouwen in de deskundigheid van statistici. Hoe complexer het model, hoe groter het geloof.
Bij de ontwikkeling van een Management Information System (MIS) kreeg ik steeds meer te maken met medewerkers van het computercentrum. In het MIS werden wiskundige modellen (in APL) en de administratie (in COBOL) samen gebracht.
Om de opslag te verbeteren werd gekozen voor het nieuwste van het nieuwste, een database-managementsysteem van IBM genaamd IMS.
De technici vertaalden deze term in Increasing MainStorage, omdat de software enorm veel geheugen kostte. In die tijd was het werkgeheugen van de computer een schaars goed. Programma’s werden vaak opnieuw gemaakt om zo slim mogelijk met geheugen om te springen. Deze optimalisatie is één van de belangrijkste oorzaken van het jaar 2000-probleem.
Het computercentrum zelf was een grote papierfabriek, waar lange lijsten werden afgedrukt en verstuurd naar de kantoren. Men besteedde veel tijd aan het omstandig aantonen, dat iets niet kon of dat de ander de schuld had van een fout.
Dit kwam, omdat men de werkwijze had opgesplitst in stappen en taken, die vaak langs elkaar heen werkten. Voordat er wat werd gemaakt moest er eerst worden opgeschreven wat er moest gebeuren. Dit laatste werd goedgekeurd door de gebruiker. Later werd de werking van de programma’s nog eens op papier beschreven. Als laatste werd er getest of de programma’s wel deden wat de bedoeling was.
In het algemeen was de gebruiker daarna niet tevreden met wat hij kreeg. Hij werd dan om zijn oren geslagen met de specificatie die hij had goedgekeurd en moest dan wel inbinden.
Het spel kostte veel meer tijd en mensen dan bij Operations Research. Veel later werd de aanpak bij Operations Research voorzien van de naam “Iteratief ontwikkelen”. In tegenstelling tot de werkwijze bij het computercentrum houdt iteratief ontwikkelen in het samen met de gebruiker stapsgewijs ontwikkelen van software. Elke korte ontwikkelstap wordt pas afgesloten na overleg met de gebruiker.
Samenvatting
- We kunnen gespecialiseerde talen naar machinetaal vertalen. Een machinetaal bestuurt een computer. Een machinetaal bevat heel weinig onderdelen en patronen. Hoe minder onderdelen en regels een taal bevat hoe meer mogelijkheden hij heeft. Gewone mensentaal voldoet niet aan de regels: zij is niet eenduidig en ze is contextgevoelig.
- Het is mogelijk om een taal te beschrijven met behulp van een andere taal. Door iedere hogere laag geven we een richting aan het toepassingsgebied. We maken de taal rijker en daarmee de uitvoer meer voorspelbaar.
- Een computer is niet in staat tot het exact uitrekenen van complexe wiskundige berekeningen. Er worden met behulp van numerieke wiskunde benaderingen geïntroduceerd, die een fout introduceren, die zichzelf versterkt als we berekeningen op berekeningen toepassen. Mensen weten dit niet of willen dit niet weten. Een computer staat voor hen voor exactheid.
- Er bestaat een groot verlangen om ideeën om te zetten naar activiteit. Een computer is het middel om dit te doen. Het overzetten lukt het beste met abstracte ideeën, die wiskundig kunnen worden beschreven. Er is dan een één op één relatie tussen denken en doen. Niet-wiskundige menselijke intelligentie is (nog?) niet te vatten in een taal. Schijnbaar gaan we als we taallagen maken ergens over een grens heen, die het onmogelijk maakt om eenduidig te vertalen.
- De problemen in de wereld laten zich in het algemeen niet vangen door een wiskundig model. Altijd moet er water in de wijn worden gedaan. Onoplosbare problemen leiden tot een groot geloof in de eigen oplossing.
- Hoe complexer het model wordt hoe onbetrouwbaarder de uitkomsten zijn en hoe groter het geloof wordt van de klant. Als een wiskundige het heeft bedacht zal het wel kloppen.
- De taal APL was ver vooruit op alle andere talen in zijn mogelijkheden. Het gemak, waarmee men een bepaald idee kan omzetten naar de werkelijkheid is bepalend voor de werkwijze. Mensen willen direct resultaat.
- Per periode is er een dominant selectiecriterium dat bepaalt wat goed en fout is. In de eerste periode van automatisering is dat de schaarste aan werkgeheugen van de computer geweest.
- Hoe meer mensen tussen de vrager naar informatie en de leverancier van deze informatie worden gezet hoe minder de resultaten aanslaan en hoe langer het ontwikkelproces duurt. Dit pleit ervoor om het “zelf te doen”.
Besturen
De hoeveelheid betrokken mensen en de omvang van de programmatuur namen in de loop der tijd toe. De afstand tussen de gebruiker en de ontwikkelaar werd groter en groter. De manager werd geroepen om orde op zaken te stellen.
De volgende fase in de geschiedenis gaat over besturen.
Het zal blijken, dat het zeer moeilijk is om de realisatie van ideeën werkelijk te beheersen.
De volgende opsomming van uiteenlopende observaties en onderzoeksresultaten hebben invloed gehad op mijn denken over en besturen van ontwikkelingsprojecten.
Planning & Beleid
In 1980 ben ik overgestapt van ABN naar de Centrale Directie van de PTT.
Hier werd ik tewerkgesteld als beleidsmedewerker bij de Centrale Afdeling Personeelsvoorziening en Loopbaanontwikkeling. De PTT was op dat moment bezig om zich op te splitsen in Geld (Giro), Post en Telecom.
De centrale afdeling was bezig met zijn “doodstrijd”. Deze strijd heeft jaren geduurd.
Om de stap van Operations Research Analist naar Beleidsmedewerker te kunnen maken volgde ik de postdoctoraal opleiding Planning en Beleid in Utrecht.
Het was de allereerste keer, dat ik theoretisch te maken kreeg met het besturen van complexe processen. Ten opzichte van Operations Research richtte ik mij nu op de mens en niet op het model.
In de opleiding liet men zien, dat het vak Planning en Beleid in een diepe crisis verkeerde. Dit was de crisis van het afbrokkelende geloof in de “maakbare samenleving”.
De bekendste onderzoeker uit die tijd was Simon, die samen met Newell het boek “Human problem solving”* (1972) had geschreven.
Een belangrijk thema in dit boek was dat de meeste problemen echt onoplosbaar zijn óf dat we onvoldoende (computer-)tijd hebben om ze op te lossen.
Mensen gaan op zoek naar het “haalbare” en relateren hun “aspiratieniveau” aan de groep, waar ze inzitten. Het is goed mogelijk, dat een oplossing slechts delen van een probleem oplost en soms elders weer grote problemen veroorzaakt. Probleem oplossen is voor een groot deel perceptie. We geloven, dat we iets hebben opgelost.
Ik zat midden tussen de beleidsmedewerkers die aan onderwerpen als Beoordeling werkten. Zij hadden hiertoe overleg met gelijkwaardige managers. Ik had niet de indruk, dat men “de vloer” bezocht.
Een korte stage bij het Postdistrict Leiden opende mij de ogen. Wat was er een verschil tussen de ideële hoogbetaalde beleidsmedewerkers en de postbeambten. Later besefte ik, dat een dergelijk contact het onmogelijk maakt om nog “beleid te maken”.
Hoe meer je weet van de werkelijkheid hoe slechter je kunt beslissen, omdat je de consequenties kent. Je hebt een abstract model en soms, letterlijk, afstand nodig om hier los van te komen.
Generaals moeten ver van het slagveld hun strategie bepalen. Soldaten zijn dan nummers en eenheden geworden. Als ze te dichtbij komen zien de generaals de mens achter het nummer en nummers kunnen niet sneuvelen, mensen wel.
Men maakt plannen als men denkt, dat de toekomst voorspelbaar is
Er was wat onderzoek gedaan naar het verband tussen het planningsproces en de toestand van de omgeving. Hierbij kwam de term “causal texture” (F.E. Emery en F.E.Trist) naar boven.
De voorspelbaarheid van de omgeving kan oplopen van “placid” naar “turbulence”. Hoe meer onvoorspelbaar een omgeving in de toekomst is hoe beter het is om ad-hoc te reageren.
Hier werd ook een mooie term voor uitgevonden namelijk “Muddling through (voortmodderen)”. Door de enorme hoeveelheid gegevens, die de laatste tijd beschikbaar komen hebben de meeste mensen het gevoel, dat de “causal texture” constant turbulent is.
Voortmodderen is de algemene trend aan het worden. Dit voortmodderen kunnen we op een nette manier vertalen in “leren en direct reageren”. De manier, waarop mensen leren is cruciaal voor het planproces.
Vandaar, dat er ook steeds meer theorieën komen, die de term leren bevatten, zoals “planning by learning” en “de lerende organisatie” (P. Senge).
In mijn scriptie voor de postdoctoraal opleiding paste ik deze theorie op de automatisering toe en beschreef het iteratief ontwikkelen van software. De toekomst is altijd onvoorspelbaar. Ze wordt gemaakt door mensen, die of denken te kunnen voorspellen of willen scheppen. “Shape your own future”!
Plannen worden uitgevoerd als iedereen de “nood”-zaak ziet.
Men deed onderzoek naar falen en slagen van grote planningsprojecten.
Een historische analyse duidde aan, dat het erg goed uitkomt als er sprake is van een ramp, zie bijvoorbeeld de Deltawerken als gevolg van de stormvloedramp van 1953.
De negatieve begrippen ramp en vijand kunnen positief vertaald worden in het begrip visie. Dit grijpt echter aan op een ander niveau. (Doods-)angst en afgunst sturen op het niveau van de emoties, terwijl een visie het intellect stuurt.
Later is me opgevallen, dat men veranderingsprocessen in het algemeen probeert te sturen met positieve denkbeelden: het voorhouden van de wortel. Het aspect pijn, de stok, laat men achterwege.
Good managers don’t make policy-decisions. They give their organizations “a sense of direction” and they are masters of developing opportunities (Wrapp, Harvard Business Review, 1967).
Plannen is verbonden aan “geloven”. Managers moeten niet zelf beslissen, maar hun medewerkers de context aanbieden om een beslissing te nemen. Er zijn mensen, die de gave van het overtuigen hebben. Het lijkt erop, dat ze dit alleen kunnen doen als ze zichtbaar en voelbaar zijn. De meeste managers zijn een naam en tonen zich niet.
Een organisatie is een samenspel van mensen. We moeten er geen individuele menselijke eigenschappen aan geven. In sommige bedrijfskundige theorieën krijgen organisaties een “eigen leven”.
Ze worden een mens en hebben een geheugen, ze leren en ze anticiperen. Voor mij is het is twijfelachtig of een verzameling mensen hetzelfde gedrag vertoont als één mens.
Een collectief heeft op hetzelfde moment over een onderwerp vele meningen. Individuen of groepen van individuen streven vaak tegenstrijdige belangen na. In grote organisaties zijn er dan ook vrijwel altijd zichtbaar of onzichtbaar concurrerende onderdelen.
Aan bedrijfskundestudenten wordt een mechanistisch beeld van de organisatie geleerd. Het topmanagement ziet de richting, drukt op de knop en de raderen draaien. Maar de medewerkers zien geen beleid en geen visie.
De omgeving blijkt niet te reageren zoals het topmanagement dacht en de raderen staan stil. Het duurt jaren voor het management, vaak na een tijdje overspannen te zijn geweest, accepteren dat het anders moet.
Organisaties zijn in de tijd onvoorspelbare, veranderende patronen van mensen en middelen en kunnen daardoor niet mechanistisch bestuurd worden.
Plannen is een mentaal proces
Mensen veranderen door de mentale en fysieke ervaringen die ze meemaken. Deze ervaringen zijn het gereedschap, waarmee ze de toekomst ingaan. Het maken van plannen wordt enorm beïnvloed door deze ervaringen.
Voorspellingen, die negatieve consequenties geven voor het toekomstig functioneren worden “weggestopt”.
Zo ziet de toekomst er in principe altijd enigszins “rooskleurig” uit. Ernstige ziekten en faillissementen overkomen anderen.
Veel methodes proberen om deze bias te voorkomen, door het toeval in het planningsproces te introduceren.
Men gaat scenario’s maken. In de mentale modellen van de werkelijkheid worden variaties aangebracht en aan de planners aangeboden. Men hoopt dan, dat iemand “het licht ziet”.
Als een kind speelt experimenteert het binnen een “veilige wereld”. Hierbij gebruikt het voorwerpen, die belangrijke zaken in de wereld voorstellen (een pop vader). Door de pop worden vele mogelijke (en ook onmogelijke) situaties uitgeprobeerd.
Ook volwassenen gebruiken dit soort manieren om zich voor te bereiden op nieuwe situaties.
Mensen lijken doelgericht, van zichzelf bewust, staan open voor de buitenwereld en hebben een eindig bestaan. In sommige theorieën hebben organisaties deze eigenschappen overgenomen.
De meeste organisaties leven echter veel korter dan mensen. Men heeft de hoop, dat planning het mogelijk maakt om de levensduur te verlengen. Arie de Geus (De Levende Onderneming) heeft laten uitzoeken wat “oude bedrijven” gemeen hebben.
Deze bedrijven blijken gevoelig te zijn voor hun omgeving, hebben een sterke identiteit, zijn tolerant en karig met geld.
Dit laatste punt is mij al meer opgevallen. Beperkingen verwekken creativiteit. Hoe minder budget hoe intelligenter de oplossing.
De identiteit maakt het voor individuen mogelijk om zich te ordenen. Men streeft naar een gezamenlijk doel. Indien de toekomst een dergelijk doel niet meer suggereert valt de identiteit weg.
Ontwikkelingen in de besturing van automatisering na 1984
In 1981 kwam ik terug bij ABN. Ik promoveerde in snel tempo naar de functie van groepsleider van een automatiseringsafdeling. In 1984 werd ik gevraagd om me druk te gaan maken over het ontwikkelproces. De projecten werden complexer.
Om de processen in de automatisering te kunnen besturen werd een aantal maatregelen genomen.
Projectmanagement werd geïntroduceerd. Dit werd gebaseerd op wat men later de watervalaanpak is gaan noemen.
Er werden scherp afgescheiden fasen ingevoerd (ontwerpen, bouwen, testen en exploiteren).
Deze specifieke fasen werden voorzien van standaarden (documentindeling, opleidingen, taakbeschrijvingen).
Men ging uit van de oude planningstheorie die een maakbare wereld veronderstelde.
Niemand had in die tijd het benul hoe snel en drastisch de automatisering en de buitenwereld zou gaan veranderen.
Er werden hulpmiddelen geïntroduceerd. De ontwikkelaar ging steeds meer tijd achter zijn beeldscherm doorbrengen. Er werd hierdoor minder tijd besteed aan overwegen.
Door de standaardisatie ging de automatisering zich voor automatisering lenen.
De eerste innovatie was de tekstverwerker, waardoor de programmeur niet meer afhankelijk was van de centrale typ- en ponskamer.
De doorlooptijd tussen idee en realisatie van het idee werd steeds korter. Bij de tekstverwerker moest men in eerste instantie nog gebruik maken van een typmachine. Later werd het beeldscherm geïntroduceerd.
Er waren minder beeldschermen dan medewerkers. Men moest inschrijven op een lijst. In de tussentijd bekeek de programmeur zijn product en op papier bracht wijzigingen aan.
In de loop der tijd werd de verhouding één op één. Vanaf toen werd er nog uitsluitend gewerkt achter het scherm. De interactie tussen computer en ontwikkelaar verving het rustig zelf nadenken.
Deze vervanging van de “contemplatie” door de interactie heeft een enorme impact op de werkwijze gehad. De mens werd langzaam maar zeker in de machine, lees de software, “gezogen”. De software nam de leiding over.
In een later stadium werd de methode vertaald in grafische hulpmiddelen. In eerste instantie vervingen die het tekenmiddel (de template). Later ging de software meedenken en taken overnemen.
De Computer Assisted Software Engineering (CASE) was geboren. De ontwikkelaars waren niet echt blij met deze ontwikkeling. Men kon zijn eigen “stijl” niet meer gebruiken.
Preventie krijgt de overhand. Dit resulteerde in vele nieuwe functies, die allemaal proberen te voorkomen dat er fouten worden gemaakt.
In 1984 werd ik verantwoordelijk voor de nieuwe afdeling Gegevensbeheer. Deze afdeling moest proberen om de samenhang in de gegevensstructuren van de bank te bewaken.
Het streven werd om een project op tijd, binnen het budget en met de gewenste functionaliteit op te leveren. Dit streven naar preventie heeft grote invloed gekregen op de werkwijze.
- Men ontdekte, dat veel functionaliteitfouten onstonden door een beperkt ontwerpproces. Het aanpassen van een ontwerp (een idee) is veel goedkoper dan het aanpassen van een programma (een realisatie). Er kwamen dus ontwerpers, die los van de bouwers gingen werken. De overdracht van de kennis van de ontwerpers naar de bouwers werd een probleem. In de loop van een project werd altijd tijd verloren. De managers durfden meestal deze uitloop niet te vertellen aan de opdrachtgevers. Men bespaarde liever tijd door “onnodige” zaken over te slaan. Er werd dan minder getest en gedocumenteerd.
- Men ontdekte, dat de ontwikkelaars zich niet aan de methode hielden. Er kwamen dan ook kwaliteitscontroleurs, verbeterprogramma’s en ISO-certificaten. De ontwikkelaars vonden manieren om aan deze controle te ontkomen. Dit gaf weer munitie aan de controleurs om hun aantal te vergroten en nog meer geavanceerde middelen te ontwikkelen.
- Men ontdekte, dat systemen elkaar in de weg zaten (overlap). Er kwamen dan ook informatieplanners en administrators, die bedrijfsdoelstellingen gingen vertalen in logische- en technische architecturen.
- Men ontdekte, dat software veel fouten bevatte. Er kwamen dan ook testers en testplannen en testhulpmiddelen.
- Men ontdekte nieuwe aanpakken en er kwam nieuwe technologie, die alles zou verbeteren. Hiertoe moesten velen vaak getraind worden.
Er kwamen zoveel verschillende soorten automatiseerders, dat het op het juiste moment bijeen brengen een probleem werd.
Er kwamen dan ook human resourcemanagers, skill-management-systemen en planningspakketten.
Het resultaat was, dat de bouwer omringd werd door een veelvoud van anderen, die feitelijk niets maakten.
Het ergste is nog, dat men nog steeds niet beschikt over een manier om objectief te meten wat productief is.
Hierdoor kon de ene na de andere hype de softwareontwikkeling in grote beroering brengen. Deze is nog steeds in afwachting van de “silver bullet”, die wellicht nooit gaat komen.
De database als grote integrator
De ontwikkelingsmethode werd sterk beïnvloed door de opkomst van de database. Het computercentrum transformeerde zich van lijstenfabriek naar opslagcentrum. Het gegeven werd uitgevonden.
De methode werd een object van heilige oorlog tussen de procesdenkers en gegevensdenkers. In essentie ging het bij deze oorlog om het verschil tussen het veranderende (gebeurtenis, algoritme, proces) en het blijvende (het gegeven, het geheugen).
De hoop bestond, dat gegevens zeer lang gelijk zouden blijven in hun semantiek en syntax. De semantiek en in het bijzonder het classificeren werd een belangrijk onderwerp van onderzoek.
Er werden projecten gestart om bedrijfsgegevens-modellen in kaart te brengen en bedrijfsbrede databases te bouwen. Deze databases moesten de waarden, betekenis en beschrijving van alle gegevens van het bedrijf bevatten.
Hiervoor deed de architect zijn intrede. Hij had als opdracht om ruimtelijke ordening tussen systemen te bewerkstelligen. De “vaste gegevens” theorie is niet uitgekomen. De werkelijkheid bevat weinig stabiele elementen.
Gegevens zijn een afbeelding van de blik van de medewerkers en de klanten op de werkelijkheid. Zowel deze blik, lees het paradigma, als de werkelijkheid zijn met toenemende snelheid aan het veranderen.
De waterval-aanpak veronderstelde stabiliteit in de verwachtingen en specificaties van de klant en in de techniek. De doorlooptijd van een redelijk project was toch gauw een jaar. In die tijd veranderde de wereld sterk.
Bij de klanten was een onderscheid te maken tussen de vertegenwoordiger van de klanten en de daadwerkelijke gebruiker van de software. De laatste kwam er bij het specificeren eigenlijk weinig aan te pas.
Als men na hard zwoegen alles klaar had begon het proces van implementatie: de eerste confrontatie met de gebruiker. In de loop der tijd is die gebruiker steeds mondiger en veeleisender geworden.
De acceptatiegraad van nieuwe software is vaak klein. Dit fenomeen komt veel minder voor bij pakketsoftware. Hier wordt goed gebruik gemaakt van marketingtechnieken. Implementeren is “verkopen”.
Het uitgangspunt bij pakketsoftware is dat het niet mogelijk is om met alle individuele wensen rekening te houden.
Men dacht structuur te zien in de bestaande situatie. Alle databases gerelateerd aan een klant werden onder één noemer gebracht net als alle manieren om rente te berekenen. Er werden vele herbruikbare elementen onderscheiden.
Deze elementen werden vertaald in een nieuwe taal, de zogenaamde 4GL. Deze taal maakte het maken van een lijst zo simpel, dat de eindgebruiker het zelf kon doen.
Een andere manier om snel te ontwikkelen is de generator. Dit is een middel om kleine stukjes bestaande programma’s aan elkaar te koppelen.
Toch bleek in de loop der tijd, dat iedere groepering op den duur weer instabiel werd. Hoe groter de samengeklonterde brokken waren, hoe moeilijker het werd om ze snel aan te passen.
De “just-in-time” ontwikkeling
De logistiek leverde het concept van just-in-time. Deze manier van werken wordt gerealiseerd door voorraden op te heffen en de ontwikkeling pas te starten als het nodig is.
Dit verreist een hoog niveau van standaardisatie en een goed inzicht in het product. Dit product wordt uit elkaar gehaald en weer opgebouwd uit instelbare bouwstenen.
Binnen de grenzen van het mogelijke worden de klanten in staat gesteld om hun wensen kenbaar te maken. Ontwikkelen wordt een proces van het instellen van soms vele parameters. Met complexe software (bijv. SAP) kan men hier maanden mee bezig zijn.
Uit het logistieke concept groeide het idee van de software-fabriek. Software wordt door de opdrachtgever just-in-time samengesteld uit pasklare onderdelen. Dit vereist een goed inzicht in het eindresultaat.
Na een aantal iteraties is een goede architect in staat om dit eindresultaat te bereiken met een beperkt aantal bouwstenen. In één keer lukt het nooit.
Een goede manier is om bestaande systemen te verbeteren. Het doel moet zijn om meer functionaliteit met minder onderdelen te bereiken.
Er wordt echter betrekkelijk weinig gekeken naar het bestaande. De meeste hulpmiddelen en methodes gaan uit van nieuwbouw. Men denkt, dat men met de nieuwe technieken en hulpmiddelen sneller klaar is met een beter resultaat.
Niet iedereen wil snel klaar zijn. Deze ontwerpers construeren bibliotheken met herbruikbare bouwstenen voor een bepaald kennis-domein.
Samenvatting
- De planningstheorie was niet voor niets in de jaren tachtig in een crisis. De wereld is niet maakbaar. Zij is door de automatisering met steeds grotere snelheid aan het veranderen. Hier bijt de slang in zijn eigen staart.
- In de automatisering heeft men er alles aan gedaan om de lering uit deze theorie te negeren. Men heeft zonder veel succes zeer zware preventieve maatregelen genomen in de veronderstelling, dat men hiermee de wereld stil kon zetten.
- In essentie gingen de bouwers gewoon door met bouwen maar nu omringd met een veelvoud van niet-productieve bestuurders. De onderlinge afstemming werd steeds complexer
- Het beperkende selectiemiddel geheugenruimte werd verwisseld voor (minimale) tijd en geld. Door de constant aanwezig tijdsdruk laat men zaken, die in het laatste deel van het ontwikkeltraject thuishoren, liggen (documenteren, testen).
- De ontwikkelaar wordt in toenemende mate verslaafd aan directe interactie met zijn ontwikkelsoftware. Iedere kleine aanpassing aan het idee kan onmiddellijk worden uitgeprobeerd. Zo wordt men steeds meer meegezogen door het detail en wordt er steeds minder tijd besteed aan het achterover leunen en contempleren.
- Het is mogelijk om na vele iteraties bekende softwarestructuren uit elkaar te halen en te versimpelen tot een aantal gekoppelde instelbare bouwstenen. Dit wordt in het bedrijfsleven vrijwel niet gedaan. Nieuwbouw is hier de meest gebruikte aanpak. Er ontstaan bibliotheken met herbruikbare onderdelen.
Groeien
De Personal Computer (PC) startte een ontwikkeling, waarbij het individu zijn gang kan gaan met automatiseren. De eigen verantwoordelijkheid voor de informatievoorziening wordt daarna steeds belangrijker.
Er komen zogenaamde softwarepakketten. Het netwerk koppelt iedereen aan iedereen en maakt het mogelijk, dat een individuele programmeur binnen korte tijd zijn programma op miljoenen PC’s laat draaien.
Software wordt niet meer ontworpen, maar lijkt te groeien. Deze groei lijkt soms op een kwaadaardig kankergezwel. Virussen tonen zich.
De kwaliteit van de software neemt af.
Individuele automatisering
Met de komst van de PC startte de individualisering van de automatisering. Het centrale mainframe rangschikte de ontwikkelaars rondom zich. Dit maakte centrale besturing mogelijk.
In de kantine en de “wandelgangen” vond veel afstemming plaats over samenhang tussen systemen en de richting die er gekozen moest worden.
De eindgebruiker zat “braaf” achter zijn terminal en deed wat de computer hem of haar aangaf. Door de PC werd dit allemaal anders.
Er werden PC-privé projecten opgezet om de nieuwe ontwikkeling bij gebruikers en ontwikkelaars te promoten. Medewerkers, die wel eens wat klungelden met de tekstverwerker begonnen te programmeren in BASIC. Een enorme verzameling niet samenhangende software begon te ontstaan.
De centrale ontwikkelafdelingen zagen hoe op vele plaatsen nieuwe software werd ontwikkeld door externe softwaremakers of door, door het management vrijgestelde, medewerkers. De concurrentie was begonnen.
De “amateurs” op de PC hadden meestal niet de kennis en ervaring van de centrale automatiseringsmedewerkers. Ze begonnen dus vrolijk opnieuw in alle valkuilen te vallen, die de professionelen net hadden gedicht. Gebaseerd op een totaal nieuwe onderlaag (Windows) begon het spel opnieuw.
Softwarepakketten vervangen maatwerk
Er komt een markt voor pakketten. Deze worden voornamelijk voor de externe klant ontwikkeld. Door de grote concurrentie neemt de snelheid van verandering en de hoeveelheid fouten exponentieel toe.
De werkwijze binnen het eigen bedrijf (hier het bankbedrijf) werd door de eigen ontwikkelafdeling als een uniek fenomeen gezien. De leverancier die probeerde om een pakket te maken voor het bankwezen moest dan ook van goeden huize komen.
Men vond altijd wel uitzonderingen, die niet in het pakket voor kwamen. In het ergste geval werd het pakket hier op aangepast en ontstond een niet onderhoudbaar software-complex.
Door deze krappe markt waren de prijzen van dergelijke pakketten hoog. Dit was ook een reden om ze niet te kopen. De PC doorbrak deze spiraal en schiep de gelegenheid om grote omzetten te gaan draaien.
Tot grote schrik van de automatiseerders werd niet de bank, maar ook de klant van de bank het object van de pakketbouwer. De interne ontwikkelaar was hier nog niet eens aan toe gekomen. Die was bezig om de interne processen te automatiseren.
Veel leveranciers zien deze lucratieve markt zitten. Door de felle concurrentie volgt de ene aanpassing de andere op. Het is voor de normale automatiseerder niet meer bij te houden.
Door de grote snelheid van ontwikkeling ontstaan zeer gecompliceerde, ondoorzichtige softwarecomplexen. De hoeveelheid softwarefouten neemt hierdoor enorm toe, maar omdat ze niet beter weten vinden gebruikers het normaal als de software per dag een aantal keren “hangt”.
Het beeldscherm krijgt grafische mogelijkheden.
De buitenkant wordt steeds belangrijker. Naast tekst komen er beelden. Er is weinig kennis over hoe een goed design moet worden ontwikkeld. De bruikbaarheid neemt sterk af. Het bijzondere van de PC zit in het grafische gebruikersinterface.
Om de een of andere reden is dit nooit voor het mainframe ontwikkeld. Met een enorme snelheid kunnen kleine puntjes (pixels) op het scherm worden aangestuurd.
Het wordt mogelijk om plaatjes en films te gaan presenteren met steeds toenemende kwaliteit.
Deze kwaliteit is sterk verbonden met de toenemende kracht van de chip in de computer. Het uitnutten van deze grafische potentie is een vak apart. De technici zijn vooral bezig om alle technische hoogstandjes uit te gebruiken. Dit heeft een sterk negatief effect op de bruikbaarheid.
Kennis wordt in software gestopt.
Men probeert kennis om te zetten in software. De adviseurs, de kenniswerkers, zijn aan de beurt om geautomatiseerd te worden.
Langzaamaan pakt de automatisering alle processen over. Het bedrijf verdwijnt letterlijk in de computer.
Men gaat proberen om kennis van experts te modelleren. Voor deze expertsystemen worden hele nieuwe talen en methoden ontwikkeld.
Na de bekende hype toont de realiteit zich. Het kennissysteem verovert langzaam de wereld en begint de kenniswerkers aan te pakken.
Er komen ondersteunende systemen voor dealers en accountmanagers. Deze laatste systemen zijn zo goed, dat ze direct met de klant kunnen gaan overleggen.
De evolutionaire aanpak.
De aanpak wordt evolutionair. Men gaat nu expliciet sturen op tijd en geld. Dit dwingt tot het stellen van prioriteiten.
De watervalaanpak verliest terrein. Men acht hem uitsluitend nog geschikt voor het ontwikkelen van infrastructuur. Veel bedrijven besluiten om deze infrastructuur te kopen.
De tegenhanger van de watervalaanpak wordt iteratief of evolutionair genoemd. Software wordt het liefst samen met de eindgebruiker in stappen (iteraties) ontwikkeld en ingevoerd. Men accepteert hiermee, dat alles niet in één keer perfect kan worden gemaakt.
Bij de methode time-boxing wordt de opleverdatum gefixeerd. Er wordt altijd wat opgeleverd. Men bespaart op de functionaliteit. Deze aanpak dwingt tot prioriseren. De theorie zegt, dat de laatste 20% van een project 80% van de tijd kost. In die tijd introduceert men de uitzonderingen die de kern van het ontwikkelde systeem aantast. Er ontstaat dan een sterke neiging om de kern aan te passen; met alle gevolgen van dien.
Netwerken koppelen iedereen aan iedereen. Er is voor alles wel een markt te vinden.
Het netwerk koppelt iedereen aan elkaar. De uitwisseling van data en programma’s neemt enorm toe.Eén mens kan de wereld veranderen.
De PC’s worden eerst door een lokaal netwerk aan elkaar gekoppeld. Daarna worden de lokale netwerken verbonden en ontstaat het World-Wide-Web.
Iedereen is theoretisch met iedereen verbonden. Het product van een slimme programmeur ergens in de wereld kan binnen een paar weken overal aan het werk zijn.
Als de invloed van dit programma negatief is noemen we het een virus. We gaan niet voor niets termen uit de biologie gebruiken.
De infrastructuur wijzigt. Er komt steeds meer functionaliteit in de infrastructuur. Er is steeds meer te koop en gratis te krijgen.
Door de keuze voor TCP/IP* als netwerkprotocol en de komst van de browser wordt het mogelijk om de infrastructuur te standaardiseren.
Dit geeft pakketontwikkelaars de gelegenheid om zelfs voor niches wereldwijd te ontwikkelen. De indruk bestaat, dat er voor alles wel een markt is. Veel ontwikkelafdelingen zien niet meer wat er om hen heen gebeurt.
Men ontwikkelt voor eigen infrastructuren en sluit de ogen voor de buitenwereld. Net als bij de opkomst van de PC kan een medewerker van een bedrijf via het Internet meer dingen doen dan hij op zijn werk kan.
Er is zoveel concurrentie, dat veel producten bij oplevering al achterhaald zijn.
De snelheid van verandering passeert de theoretisch haalbare ontwikkeltijd. Ontwikkelen wordt gokken op meerdere paarden of de concurrentie volgen.
Tot voor kort was het mogelijk om een zet van de concurrentie te pareren door snel een eigen project te starten. De veranderingen gaan nu zo snel, dat de resultaten van een dergelijk project bij oplevering meestal al weer zijn verouderd.
Om als eerste in de markt te komen moet men dus ver voor de markt uitlopen. Men moet op meerdere ontwikkelingen tegelijkertijd gaan gokken of volger van de markt worden.
De hoeveelheid mislukte projecten neemt toe.
Daarnaast wordt ook steeds meer nieuw ontwikkelde software niet in productie genomen, omdat ze al is achterhaald. Dit resulteert in grote verliezen.
Weinig bedrijven kunnen of durven deze aanpak aan. Men gaat over tot het opkopen van succesvolle starters. Op deze manier draagt de maatschappij de kosten. Minder dan 20% van deze starters heeft succes.
Naast deze chaos ontstaat er ook ordening, doordat een aantal zaken standaard worden.
Deze standaarden worden niet meer door instituties gemaakt (bijv. ISO), maar ontstaan doordat een bedrijf een groot marktaandeel pakt. Helaas voor velen is dit bedrijf steeds Microsoft. Hier heeft men zich gespecialiseerd in het manipuleren van de markt.
Indien dit nodig is stopt men van de ene op de andere dag een ontwikkelproject en probeert hiermee een onvoorziene ontwikkeling in de markt in te halen. De kleine software-ontwikkelaars volgen dit spel met argusogen. Als ze te laat reageren zijn ze uit de markt. De markt lijkt op een zwerm vogels, die op zoek zijn naar een plek om te overnachten.
Samenvatting
- De PC geeft de gebruiker het heft van de automatisering in handen. De centrale automatiseringsafdeling, toch al kampend met een slecht image (luistert niet, duurt lang), wordt bestookt door toenemende concurrentie van softwarebureaux en pakketontwikkelaars.
- Door de toevloed van nieuwe ontwikkelaars en gebruikers ontstaat een explosie van nieuwe software, die in het algemeen van slechte kwaliteit is. Daarnaast werkt veel van deze software niet goed samen met de rest. De interfaces zijn slecht of niet gedefinieerd.
- De ontwikkelaanpak maakt gebruik van tijdsdruk en wordt iteratief. Om te voorkomen, dat er veel tijd wordt besteed aan uitzonderingen, die de structuur van een systeem verstoren, wordt het oplevertijdstip en het budget gefixeerd.
- Het koppelen van PC aan een netwerk geeft een enorme versnelling aan het ontwikkelproces. Eén programmeur kan binnen korte tijd zijn software bij velen op de PC brengen.
- Het selectiecriterium tijd en geld wordt vervangen door functionaliteit. De ontwikkelafdelingen kunnen niet snel genoeg meer reageren op een ontwikkeling. Men moet gaan anticiperen en gokken.
- Hoe sneller de ontwikkelsnelheid hoe groter het verlies aan functionaliteit. Er wordt steeds meer voor niets gewerkt en weggegooid.
- Standaardisatie vindt plaats door de markt te veroveren. Dit lukt door razendsnel op de markt te reageren. Dit betekent, dat men snel iets moet kunnen starten en stoppen. Dit laatste is het grootste probleem.
Overzicht van de ontwikkelingen 1970 – heden
Fase 1: Programmeren
Het begint allemaal met programmeren (doen).
Fase 2: Besturen
Door de toenemende grootschaligheid ontstaat een crisis en de behoefte om te besturen. Men gaat steeds meer preventief te werk en laat het bouwen vooraf gaan door denken.
Er komen steeds meer managers en controleurs. Men denkt alles te kunnen vatten in een methode. Deze methode wordt omgezet in hulpmiddelen. Er worden generatoren bedacht en bouwstenen gevonden. Door het gebrek aan objectieve meetinstrumenten weet men niet of men beter wordt van een verandering. De ene na de andere hype slaat toe en kost veel veranderingstijd. Aan het eind van de rit blijkt er niet veel veranderd te zijn.
Fase 3: Groeien
De PC maakt het voor de eindgebruiker mogelijk om zaken zelf op te pakken (eigen verantwoordelijkheid). Door de enorme verspreiding van de computer wordt het bovendien mogelijk om pakketten te ontwikkelen. Deze zijn door iedereen te betalen en leveren de leverancier grote winsten op.
Het verspreiden van het ontwikkelproces naar de eindgebruiker levert chaos op. Het gebruik van pakketten geeft voordeel.
Door het netwerk wordt iedereen aan iedereen gekoppeld. Een individu kan binnen enige weken zijn software op miljoenen PC draaiende krijgen. De bruikbaarheid van de software en de stabiliteit bereiken een dieptepunt.
De versnelling van het proces bereikt zijn hoogtepunt. Bedrijven moeten kiezen voor grote investeringen met geen of erg veel rendement of voor het volgen van de concurrentie
De drie fasen geven een kijk op een explosie van functionaliteit: van de individuele programmeur, via het project en de lopende band, waar softwarebouwstenen aan elkaar worden geplakt naar de huidige software-explosie; van het statement naar steeds hogere ordeningen in het softwarecomplexen.
Er zijn steeds meer mensen steeds losser en verder van elkaar bezig om een samenwerkend geheel te maken.
Het besturen van deze mensen met plannen en architecturen lukt niet. Ze laten zich niet sturen.
De druk om zelf te maken is zeer sterk. Dit wordt nog eens versterkt door de verwachting van groot geldelijk gewin (“the killer application”).
We zullen op zoek moeten gaan naar een manier van besturen door iedereen zijn gang te laten gaan. Eerst gaan we eens kijken naar hoe mensen omgaan met complexe structuren.
De mens
Mensen leven in een structuur in. Ze hebben vaak “last van een geloof”..
Daniel Denett* probeert in zijn boek “Conscience explained” uit te leggen hoe het bewustzijn in elkaar zit. Volgens hem lijkt het bewustzijn op een verzameling vrienden en kennissen, die een spelletje spelen.
Ze sturen er één de kamer uit met de opdracht om bij terugkomst de verborgen betekenis te vinden. De groep mag alleen Ja of Nee antwoorden. Zodra speler weg is wordt afgesproken om at random te antwoorden.
Bij een vraag die begint met de letters a t/m m geeft men Ja als antwoord en anders Nee.
De lol van het spel is, dat de persoon in kwestie altijd een betekenis vindt, die men van tevoren nooit had verwacht.
Men wordt gevangen door de ideeën die door het JA/NEE-spel opkomen en maakt er een coherente structuur van.
Complexe structuren fungeren als de verzameling vrienden en kennissen. Na enige tijd denken we ze “door te hebben” en vertellen we er een coherent verhaal over.
Ons bewustzijn voelt zich genoodzaakt om ordening aan te brengen. Hierbij geldt de bestaande ordening als uitgangspunt. Wat we kennen is bepalend voor hoe we het nieuwe interpreteren.
Een grote langzaam verlopende verandering in de tijd wordt meestal (te) laat gezien, omdat men zijn interpretatie niet kan aanpassen. Grote plotselinge veranderingen geven uitval (shock). Het bewustzijn kan dit blijkbaar niet aan.
Een analist gebruikt zijn oude kennis om de nieuwe kennis te vergaren.
Een persoon die lang in een bepaalde context doorbrengt wordt één met deze context.
Het observeren van de complexiteit van een bepaald fenomeen of een situatie is persoonsgebonden. Wat de één simpel vindt, vindt de ander razend ingewikkeld. Hoe langer men met iets omgaat hoe meer structuur men ziet en hoe meer men complexiteit reduceert. Dit doet men door de structuur in te pakken in een simpele bekende structuur.
Een softwarecomplex wordt voorzien van een naam en omschrijving, die min of meer de vermeende lading dekt (het operating systeem of het internet). Met deze beschrijving wordt nu driftig verder gewerkt op het niveau van de concepten.
Zo is het mogelijk om complexen planmatig te koppelen en te herzien zonder, dat iemand inzicht heeft in de werkelijke mogelijkheden en onmogelijkheden. Alles gebeurt theoretisch met behulp van de modellen die men in zijn hoofd heeft.
Mensen zijn instaat om met grote structuren te manipuleren zonder enig inzicht te hebben in de interne werking van deze structuren. We geloven het letterlijk wel!
Als we een ingepakte gelaagde structuur weer uitpakken verwachten we laag na laag de indelingen en principes van de topstructuur. In de praktijk zijn diepere lagen totaal anders. Zo verklaren de meeste mensen alles met alles.
Mensen zitten in hun denkwereld gevangen. Innovatie is van buiten naar binnen kijken.
Het beeld van de werkelijkheid is ingepakt door de gebruiker. Deze heeft geen werkelijk zicht meer op zijn werkomgeving.
Een analist probeert zich in de denkwereld van zijn klant te verdiepen. Hij doet dit door deze denkwereld van boven naar beneden laag na laag in kaart te brengen.
De gebruiker “liegt” en verklaart alles met principes, die alleen op het hoogste niveau opgaan.
De analist brengt niet het systeem in kaart, maar de interpretatie van de gebruiker die zich midden in het systeem bevindt.
Het is zeer waarschijnlijk, dat ieder een ander beeld heeft van de werkelijkheid. We denken, dat we in staat zijn om op “exacte wijze” over deze beelden met elkaar te communiceren. Deze communicatie geeft ons het gevoel, dat we hetzelfde observeren.
We kunnen alleen innoveren als we buiten naar binnen werken of een ons permanent open stellen voor onze neiging om te verstarren (“een open mind”). Managers moeten hun medewerkers hier op aanspreken en tot voorbeeld zijn.
Mensen zijn overlevingsmachines. .Een bedreiging die zich op lange termijn voordoet wordt ingepakt/ weggestopt. Mensen houden van graduele aanpassing.
Veel van mechanismen, die de mens onmiddellijk paraat heeft zijn gericht overleven. Als het echt nodig is overrulen ze alle andere processen en passen onze perceptie aan. Als alles rustig zijn gang gaat zien we de veranderingen niet meer. Bekend is het verhaal van de levende kikker die zich zonder problemen liet koken in een langzaam opwarmende pan.
Ideeën besturen mensen
Ideeën besturen de mens. Net als genen.
Sommige ideeën hebben een grotere kracht dan andere. De term “meme” heeft Denett gebaseerd op het begrip “gene” (gen). Dit om aan te duiden, dat er op het niveau van concepten vergelijkbare evolutieprincipes spelen, als op het niveau van de genen.
Concepten zijn volgens hem een vanzelfsprekende opvolger in het evolutieproces. Conceptstructuren ontwikkelen zich net als de soorten zonder bemoeienis van de mens. De mens fungeert als transformator. Memen kunnen zich nog niet buiten de mens om voorplanten.
Concepten worden bij het ontwerpen vertaald in objecten en algoritmen. Dit betekent, dat de invloed van het evolutieproces van de memen ook in de softwareontwikkeling zichtbaar zou moeten zijn.
Het feit, dat we invloed van de memen op ons functioneren niet zien is verklaarbaar. Mensen kunnen er niet goed tegen om het gevoel te hebben, dat ze geen beheersing hebben over hun omgeving.
Het gaat hierbij zover, dat men de waarheid aanpast (“liegen”). Dit “liegen” moeten we niet verwarren met het intentioneel niet de waarheid vertellen. Men is zich er niet bewust van. Het besturen van mensen moet worden gebaseerd op kennis van de manier, waarop meme’s de mens sturen. Een manager moet zijn mensen verleiden, manipuleren, hypnotiseren etc. Helaas hebben deze woorden tot op heden een negatieve bijklank.
Ideeën gaan voor het denken uit. Mensen zijn bang om te falen.
Excellente ontwikkelaars denken niet na, maar vertrouwen op hun intuïtie. De Indiase filosoof Sri Aurobindo zegt in een brief (“Letters of Sri Aurobindo 3rd series 1949”)* het volgende:
“Het intellect is een onzinnig overactief deel van de natuur; het denkt altijd, dat er niets goed gedaan kan worden tenzij het een vinger in de pap heeft, en daarom rijdt het instinctief de inspiratie in de wielen, blokkeert deze voor de helft of voor meer dan de helft, en stelt alles in het werk om zijn eigen minderwaardige moeizame producten in de plaats te stellen van het ware spreken en het ware ritme dat had moeten komen. De dichter ploetert vertwijfeld rond om het ware woord te vinden, het authentieke ritme, de werkelijke goddelijke substantie van wat hij te zeggen heeft, terwijl het de hele tijd kant en klaar daarachter ligt te wachten”.
De opkomst van een idee gaat voor het denken uit. Het denkproces haalt het idee uit elkaar en analyseert de consequenties van het uitvoeren van het idee.
Denken is een middel om het gevaar op korte termijn in kaart te brengen en te bezweren. Goede ontwerpers en programmeurs (meestal zitten ze samen in één persoon) zijn pas na het maken van het programma in staat om hun werkwijze te verklaren.
Ze hebben een “direct link” tussen de ideeëngenerator en de programmamaker in hun hersenen. Hoe beter de programmeertaal dit toestaat (APL!) hoe beter het gaat. Het toepassen van een methode of het documenteren zien ze als mosterd na de maaltijd.
We moeten de intuïtie van mensen meer ruimte geven door ze het gevoel te geven, dat ze mogen falen.
Een groep mensen moet zichzelf besturen. Hoe verder men afstaat van de werkelijkheid hoe meer het beeld verandert en verslechtert
Het besturen van ontwikkelingen heeft twee kanten namelijk het besturen van de structuur, zoals de bestuurder die ziet en het besturen van de personen die deel uitmaken van de structuur.
Veel bestuurders denken, dat hun medewerkers hetzelfde weten en denken als zijzelf. Dit is vrijwel nooit het geval. Bestuurders steunen meestal sterk op denkbeelden, die hén succesvol hebben gemaakt. De consequentie is, dat medewerkers in het algemeen de opdrachten van hun bazen niet goed uitvoeren.
De bazen verklaren deze houding van hun medewerkers vanuit: “ze willen niet”. Aan dit spel der verbeelding kan erg veel tijd en geld worden besteed.
Het besturen van een complexe structuur met een hiërarchie die zich niet kan verdiepen in de denkwereld van de ontwikkelaar werkt niet.
Op dit te voorkomen zijn managementprincipes bedacht als “management-by-walking-around”. De meeste managers blijven echter liever in hun werkkamer zitten of versterken hun beeld van de wereld door met collega-managers te overleggen.
Op deze wijze scheppen zij het “zwarte-management-gat”. Bij grote ontwikkel- en beheerprojecten is de perceptie van de bestuurder in het algemeen sterk afwijkend van die van de ontwikkelaars. De status en de voortgang van het project zijn niet echt bekend bij de bestuurders. Dit alles pleit voor “zelfsturende” teams. Deze teams moeten worden gemanipuleerd door ideeën.
Top-down ontwikkelen mislukt vrijwel altijd. De (denk-)wereld bestaat uit vele los -samenhangende en vaak overlappende structuren. We kunnen geen alomvattende systemen bouwen.
Het top-down uitwerken van een complexe structuur met een consistent principe mislukt. De reden is dat we op een bepaald ogenblik op een anders gestructureerde laag stuiten en het niet aandurven om het verklaringsprincipe aan te passen. De A-schematechniek van ISAC is door deze reden nooit bruikbaar geworden.
Gegevensmodellen op een hoog abstract niveau zijn in niet in één slag te detailleren naar het allerlaagste niveau. Ergens gaat het mis.
Als we de juiste aanpassingen hebben aangebracht en de zaak weer “naar boven” proberen sluitend te maken treedt hetzelfde probleem op. De abstracte structuur klopt niet. We pendelen dan van boven naar beneden in de abstractie.
Een ervaren ontwikkelaar begint er gewoon niet meer aan. Het beste is om middenin te beginnen en de botsing van de opgesplitste niet aansluitende eenheden af te wachten en dan pas af te handelen.
Het is trouwens niet op voorhand duidelijk wat middenin is. Er is een wet van behoud op het niveau van de objecten en regels. Hoe minder objecten, hoe meer regels. De meeste mensen zien de regels niet.
Hierdoor is het aantrekkelijk om bij de topstructuur te beginnen. Regels worden pas veel later in het proces toegevoegd. Top-down ontwikkelen is nog steeds de meest gebruikte aanpak.
Hierdoor worden er veel niet passende structuren ontwikkeld, zodat er op de lange termijn veel moet worden aangepast. De top-down structuur blijft dan vaak dan in concept in leven en vormt de verklaring voor het complex.
Het mislukken van de besturing over een proces wordt meestal niet gezien of zelfs bewust verborgen, omdat dit tot teveel statusverlies leidt. We moeten streven naar software, die zich beperkt tot een kennisdomein. Hierbij geldt de regel beter te klein dan te groot.
Er is een geloof in de perfecte aanpak, die morgen komt. Men moet niet te snel veranderen. Verbeter wat er is. Soms is het nodig om kapot te maken. Het systeem is oud.
Sommige ideeën hebben een zeer sterke aantrekkingskracht. Ze gaan “als een lopend vuurtje” door de samenleving en worden door velen als verklaring gebruikt.
Door de massamedia wordt dit proces versneld. Het lijkt erop, dat ideeën sneller opkomen en sneller uitsterven. Dezelfde ideeën komen net als een virus terug, maar vaak onder een andere naam.
Een aantal zeer oude verworvenheden in de softwareontwikkeling worden stelselmatig opnieuw uitgevonden nadat een nieuw concept heeft gefaald. In de huidige periode zijn we gevangen door de PC en het daarmee samenhangende “client-server”-concept. Duidelijk mag zijn, dat de PC perfect past in het principe van “total-control”.
Vele PC’s aan elkaar gekoppeld door een netwerk lijken erg veel op een mainframe met parallelle processoren. We kunnen dus veel ervaring ontlenen aan het ontwikkelen voor het mainframe. Toch begon iedereen opnieuw het wiel uit te vinden.
Een tragisch voorbeeld zijn de performance-problemen bij Client-server-applicaties, die veroorzaakt worden door niet geoptimaliseerde gegevensstructuren.
Automatiseerders houden niet van herhaling. Ze zoeken de kick in het steeds opnieuw beginnen.
We vinden deze observatie terug in de beroemde uitspraak over de “silver-bullit” uit 1982 van P. Brooks in zijn boek The Mythical Man-month (“There are no simple, easy-to-implement answers for excellence in software-development“).
Soms is het nodig om radicaal opnieuw te beginnen en alle “heilige huisjes” te vernietigen. Toch komt ook dit proces vaak neer op het verplaatsen van bouwstenen, waardoor een ander perspectief ontstaat.
Samenvatting
- Na enige tijd verzinnen mensen altijd een verklaring voor iets. In deze verklaring gaan ze leven. Als er niet iets dramatisch verandert, zien ze de wereld niet meer veranderen.
- Ideeën sturen mensen. We noemen dit intuïtie. “Denken” gebeurt pas na ideeënvorming en werkt voor een groot deel preventief: het vermijdt dat we falen. We kunnen de intuïtie stimuleren door falen niet af te straffen.
- We denken, dat anderen onze motivatie altijd goed snappen. Dit komt omdat we geloven dat iedereen dezelfde zaken meemaakt en dezelfde wijze van redeneren heeft.
- Hoe verder men van een proces afstaat hoe slechter het beeld. Men kan een proces alleen besturen als men er midden instaat. Dit vraagt om “zelf-sturende” teams.
- Mensen zijn overlevingsmachines. Een simpele structuur is niet bedreigend en een complexe structuur kan bedreigend zijn. Een bedreiging die zich op lange termijn voordoet wordt ingepakt/ weggestopt. Mensen houden van graduele aanpassing.
- Op elkaar lijkende structuren kunnen een totaal ander verklaringsmodel hebben. Dit kan soms aan een onbeduidende variabele liggen. We moeten veel vaker opnieuw beginnen.
- Een topdown analyse schiet altijd door. We moeten tot inzicht komen door op- en neer te gaan in een structuur. Zo ontdekken we de echte contouren.
- Er is een geloof, dat morgen alles beter wordt. Men is geneigd om nieuwe aanpakken ongetest op grote schaal op te pakken. Het is beter om wat men heeft te verbeteren. Als het echt niet meer gaat moet men wat men heeft in stukken hakken en deze stukken op een andere manier weer aan elkaar lijmen.
De evolutie-theorie
Wat is evolutie?
Een evolutionair proces moet altijd ergens in plaatsvinden. We noemen die plaats het universum. We kunnen daarbij denken aan de werkelijke wereld, maar ook aan een computer of het brein.
De karakteristieken van het universum bepalen het evolutionaire proces dat er plaats vindt. In het universum moet er iets zijn, waar evolutie op wordt toegepast, een substantie, zoals materie of ideeën. Evolutie maakt van deze substantie complexe structuren. Deze structuren passen zich aan.
Om aanpassing mogelijk te maken zijn er twee mechanismen nodig, n.l. variatie en selectie. De eerste verandert structuren random. Het variatiemechanisme weet niets van het bestaan van de structuur. Het variatiemechanisme behoort bij de structuur.
Selectie bepaalt welke veranderde onderdelen van de structuur behouden blijven. Ook de selectie weet in het algemeen niets af van de structuur.
Als we naar de natuur kijken kunnen we in structuren lagen onderscheiden, die in meer of minder mate onderhevig zijn aan evolutie. Hoe meer de laag is ingekapseld hoe minder hij zich aanpast of anders gezegd hoe stabieler hij is. De buitenlaag beschermt de binnenlaag.
De lagen communiceren met elkaar. We zouden kunnen stellen, dat de buitenlaag het universum vormt voor de binnenlaag. Binnenstructuren veranderen veel langzamer dan buitenstructuren. Ze zijn “klaar” met evolueren.
In een universum kunnen zich meerdere structuren bevinden, die naast elkaar opereren. Een evoluerende structuur kan deel uit maken van een selectiemechanisme van een andere structuur. We hebben de neiging om evoluerende structuren te groeperen. Het is de vraag of deze ordening bijdraagt aan de verklaring van wat er gebeurt.
We kijken bijvoorbeeld naar structuren, die elkaar “in de weg zitten” of die geen invloed op elkaar uitoefenen. We kunnen structuren in de tijd bekijken. We noemen ze dan generaties.
Selectie kan in verband worden gebracht met schaarste (in geld en tijd). Hoe minder mogelijkheden er zijn om de problemen op te lossen hoe sneller men gedwongen wordt een sprong te maken naar een ander universum. In het algemeen schept “ongebreidelde” vrijheid geen enkele structuur.
Organisaties hergedefinieerd met behulp van de evolutieleer.
Als we de biologie gebruiken als denkwereld lijkt een organisatie op een soort naarmate de medewerkers meer op elkaar lijken. Hier komt het principe van de “identiteit” bij De Geus naar boven. Wat we willen is de soort zo lang mogelijk in stand houden. We willen heel lang hetzelfde zien. Dit stelt ons als mens gerust.
Soorten evolueren snel als er veel veranderingen optreden in de omgeving en als er een hoge mate van interactie is tussen de individuen op fysiek niveau (kunnen bewegen) en mentaal niveau (kunnen communiceren met tekens). Zodra de soort er echter erg veel anders uitziet noemen we hem anders. Dit geldt ook voor organisaties.
De transitie van de ene naar de ander soort gaat bij organisaties gepaard met zeer complexe rituelen (faillissement). In essentie blijft er altijd wel ergens een verzameling mensen en memen bijeen.
Om een organisatie in stand te houden moet men niet teveel veranderingen oppakken en de interne communicatie niet reguleren. Beide zaken komen neer op het aanbrengen van een afscherming naar buiten en het afschermen van de communicatie tussen mensen. Duidelijk zal zijn, dat een dergelijke organisatie op termijn dood gaat.
Langlevende organisaties zijn dat door mazzel, bijvoorbeeld doordat hun externe omgeving lang gelijk blijft. Het gaat er om, om bij geleidelijke veranderingen op tijd schotten weg te halen en/of te verplaatsen.
De evolutieleer toegepast op software
Richard Dawkins beschrijft het evolutieproces in zijn boek “The blind watchmaker” als volgt “ We have seen that living things are too improbable and too beautiful “designed” to have come into existence by chance . The answer, Darwin’s answer, is by gradual, step-by-step transformations from simple beginnings, from premordial entities sufficiently simple to have come in existence by chance“.
In dit groeiproces ontstaan min of meer stabiele lagen (soorten), die als startpunt fungeren voor een diversificatie. De transformatie wordt bepaald door een selectiemechanisme, dat op den duur overleven of sterven bepaald.
Het ontwikkelen van complexe software-architecturen kan gezien worden als een graduele transformatie van programma’s gestuurd door een selectiemechanisme. Dit mechanisme heeft nu nog via de mens, op het individuele niveau, zijn werking.
Ik schrijf nadrukkelijk “nu nog via de mens”, omdat ik het niet voor onmogelijk houdt, dat het groeiproces ook zonder kan. De komst van de computer biedt de evolutie de mogelijkheid om het groeiproces te parallelliseren.
Het selectiemechanisme is in de loop der tijd veranderd. Eerst werd er gelet op een minimaal geheugengebruik. Daarna werd “het op tijd zijn” de belangrijkste factor. Nu dit niet meer lukt is de functionaliteit van de software zelf van belang. We kunnen zaken makkelijker vervangen dan vroeger. Dit hangt samen met de weg die software is gelopen. Van de computer, via het project naar de gebruiker
De diepere infrastructurele lagen van de software (bijv. het operating systeem) hebben zich genoeglijk ingepakt. Zij laten de buitenste lagen de druk van de variatie opvangen.
Evolutie volgens Kauffmann
Richard Kauffmann vindt de verklaring van Dawkins niet voldoende. In zijn boek “The origins of order” toont hij aan, dat ordening een eigenschap is van bepaalde zichzelf reproducerende netwerkstructuren.
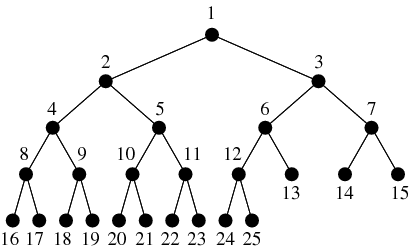
Belangrijk zijn de verhouding tussen het aantal verbindingen, het aantal knooppunten en de mate van terugkoppeling in het netwerk. Netwerken met gemiddelde twee verbindingen per knooppunt vertonen vanzelf een hoge mate van ordening.
Hoe meer koppelingen hoe lager de ordening. Netwerkstructuren kunnen in de tijd convergeren, divergeren en trillen op de grens tussen orde en chaos Deze laatste toestand is de meest adaptieve toestand. De drie toestanden zijn te vergelijken met vaste stof, gas en vloeistof.
Kaufmann’s theorie is toepasbaar op vele structuren, van het DNA tot de maatschappij. We definiëren nu een idee->mens->software-combinatie. De mens fungeert als een transformatiestation.
Het totale netwerk kan een ordening gaan krijgen, instabiel worden of op de grens van de chaos gaan verkeren (Kaufmann) en zich door een selectiemechanisme gradueel aanpassen (Dawkins/ Denett*).
Het netwerk bevat terugkoppeling. Kaufmann’s boek gaat voor het grootste deel over de biochemie, maar in een tweetal bladzijden probeert hij zijn theorie uit op technologie transfer en concepten.
Hij komt tot de volgende conclusies:
- Hoe meer verschillende knooppunten in het netwerk worden gekoppeld hoe meer diversiteit er ontstaat.
Dit verklaart de enorme diversiteit van software door de komst van de PC. We kunnen nu voorspellen, dat het Internet een nog grotere diversiteit zal geven, die wellicht zal omslaan in een chaotische toestand. Hoe meer mensen met andere culturen in aanraking komen hoe groter de diversiteit aan concepten. Dit kan leiden tot structuurloosheid en chaos.
- Hoe verder men in de toekomst plant hoe meer diversiteit er ontstaat.
Ad-hoc werken geeft sterke ordening en uiteindelijk stilstand. Het systeem kan niet meer reageren op grote veranderingen in de omgeving. Door te spelen met de termijn van planning kunnen we de groei van het netwerk beïnvloeden.
- Hoe beter een systeem ontworpen is, hoe kwetsbaarder het is voor verandering.
Deze regel pleit er voor om ontwerpen te maken, die niet precies passen op het op te lossen probleem. Een hoge graad van redundantie vermindert de kwetsbaarheid. Wellicht moet er toch meer op “z’n beloop gelaten worden”.
- Er komen altijd verstoringen voor.
Dit is de wet van Murphy. Er zit trouwens wel regelmaat in het voorkomen van dergelijke foutsituaties. Het is nodig om dit te weten, omdat men anders gaat zoeken naar oorzaken, die er niet zijn. Bij mijn weten is er op dit gebied nog geen onderzoek gedaan.
- Hoe beter het model van de werkelijkheid hoe chaotischer het gedrag.
Het loont helemaal niet om informatiesystemen te verbeteren. Uiteindelijk kan een onderneming aan een perfecte informatievoorziening ten onder gaan. Alles weten is niet goed voor een mens. We zullen het besturingsmodel van de onderneming en de mens eens op deze inzichten moeten aanpassen.
Spelen met tussenschotten, lagen en stromen
Het wordt tijd om tot een conclusie te komen. Aan de hand van de geschiedenis van de automatisering zijn we van bouwen, via besturen bij groeien aangekomen.
Hierbij moet groeien worden gezien als een continu proces van ontstaan, ontwikkelen en sterven van steeds nieuwe soorten.
De productie aan software is zo groot en onsamenhangend geworden, dat we mee moeten gaan met de stroom.
Er komt software op ons af, die we niet eens willen ontvangen (virussen).
De evolutietheorie zou bruikbaar moeten zijn om de softwarewereld te beschrijven. In dit hoofdstuk probeer ik te spelen met denkbeelden over netwerken en te komen tot een manier om te zaak te kunnen hanteren.
Het netwerk is een belangrijk concept aan het worden
Zowel in de automatisering, als in de biologie en de cognitiepsychologie is het netwerk een belangrijk concept aan het worden.
In de verschillende wetenschappen zijn de knooppunten (computers, genen en neuronen) anders van inhoud. Toch worden gelijksoortige conclusies getrokken. Door het netwerk stroomt informatie. Deze informatie wordt gedragen door een medium (electronen, RNA).
Structuur ontstaat door weloverwogen met koppelingen om te gaan en de terugkoppeling in het netwerk te regelen. Door “schotjes” tussen compartimenten te plaatsen of weg te halen ontwikkelen delen zich alleen of samen.
De informatie stroomt dan via andere kanalen. Soms lopen paden dood. Andere paden sluiten in zichzelf: een “loop”. Gekoppelde delen streven naar een evenwicht. Soms lukt dit niet en wordt het patroon (tijdelijk) chaotisch. Het netwerk kan zich hierdoor aan een observator vast, vloeibaar (beweeglijk) en chaotisch van structuur tonen.
De meest flexibele structuur is vloeibaar. In vloeibare toestand kan een deel van het netwerk structuur hebben en een ander deel chaotisch zijn.
Een vloeibare structuur kan zich snel reconstrueren en instellen op veranderingen in de buitenwereld. Een kleine verandering kan een gestructureerd gebied op grote schaal van structuur doen veranderen. Sommige gebieden zijn bestand tegen veranderingen. Ze herstructureren pas na grote druk.
Netwerken van mensen
Als we van mensen en hun communicatie een netwerk maken ontstaan organisaties en projecten. Dit zijn patronen, die geruime tijd blijven bestaan.
Ze blijven langere tijd in stand, omdat ze zichzelf reproduceren en bestand zijn tegen veranderingen. De structuur van het netwerk bewerkstelligt dit. Er is een afbakening gemaakt tussen binnen en buiten.
De mensen hebben een bril op gekregen, die ze het idee geeft, dat de binnen- en buitenwereld stabiel is of voorspelbaar verandert. Deze bril noemen we vaak cultuur of visie.
Door de komst van communicatienetwerken worden steeds meer connecties tussen mensen gemaakt. Dit resulteert in andere bestendige patronen dan de huidige. We noemen deze patronen netwerkorganisaties.
De afscherming tussen bedrijfsonderdelen door een hiërarchie werkt niet meer. De “top” wordt hierdoor geïsoleerd van zijn onderlaag. Projecten transformeren zich in “autonome teams”, die zich in onderling overleg specialiseren in een bepaald productieproces.
Een flexibel mensennetwerk is vloeibaar
Een vloeibare mensenstructuur is een structuur die bijna uit elkaar valt.
Indien een team langdurig een vast patroon vertoont, moet de manager zorgdragen voor nieuwe “losheid”. Menselijke structuren hebben nu eenmaal de neiging om te verstarren.
Het is niet de bedoeling, dat managers structuren permanent “kapot maken”. Dit geeft stress.
Indien een structuur doelgericht werkt is vastigheid een noodzaak. Soms kan het verplaatsen van één medewerker al nieuwe vloeibaarheid bewerkstelligen (“never change a winning team”).
Een mensennetwerk deelt concepten. Een stabiele mensenstructuur betekent een stabiel patroon van data-uitwisseling en daardoor gedeelde concepten.
Concepten veranderen mensen en mensen veranderen concepten. Hoe meer koppelingen er komen, hoe meer concepten zullen worden gedeeld. Er ontstaat een evenwichtstoestand.
Ook hier moet iemand de evenwichtstoestand verstoren als binnen- en buitenwereld teveel van elkaar gaan afwijken. Mensen hebben de eigenschap om hun beeld van de buitenwereld aan te passen aan hun binnenwereld.
Netwerken van concepten
In het boek ” Fluid concepts and creative analogies (1995)” doet Hofstadter verslag van zijn experimenten over “Fundamental mechanisms of thought”.
Creativiteit is volgens hem een product van “subcognitive pressure” that probabilistically influence the building and reforming of representations […] Cognititive representations are relativily immune to contextual pressure […] A crucial role is played by the inner structure of concepts and conceptual neighborhoods”.
Creativiteit verschijnt door het uitoefenen van druk, waardoor er foutjes ontstaan in meestal stabiele structuren (“slips of the tongue”). Deze stabiele structuren bestaan uit concepten met hun omgeving.
Nieuwe concepten ontstaan in mensen onder druk. Ze komen meestal spontaan in mensen op na een periode van spanning. Op het juiste moment tijdens het examen komt een briljante inval. Kunstenaars maken gebruik van deze aanpak om bijzondere dingen te laten ontstaan. Inspiratie resulteert helaas niet altijd in briljante ideeën. Niet alle foutjes zijn bruikbaar net als in de evolutie.
Sommige mensen krijgen vaak briljante invallen. Ze combineren onbekende gebieden.
Sommige mensen hebben meer dan anderen last van briljantie. We noemen ze wonderkinderen of genieën. Vaak hebben ze interesse in vele haaks op elkaar staande vakgebieden. Ze brengen nog onbekende combinaties tot stand, zodat er letterlijk een nieuwe vonk kan overspringen. Naast briljante mensen zijn er mensen nodig die de gaten vullen, die door de voortrekkers zijn gemaakt.
Concepten veranderen via mensen de werkelijkheid
Aansprekende concepten verleiden mensen tot realisatie. Deze realisatie vindt plaats in de wereld waar men deel van uitmaakt. Men zet de componenten die men kent en een beperkt aantal nieuwe, in de gewenste volgorde. Vaak zijn er standaardpatronen om een passende volgorde te bewerkstelligen.
Realisatie blijkt plaats te vinden via vaste patronen
De architect Christopher Alexander heeft veertien jaar gewerkt aan het boek ” The Timeless Way of Building” (1979).
Het boek gaat over het ontwerpen en realiseren van drie dimensionale structuren, zoals een tuin, een gebouw of een stad die beschikken over “Quality without a name “. Dit begrip is wellicht het best te beschrijven met “het gevoel, dat het goed zit”.
“Quality without a name” ontstaat door het gebruik van “design patterns ( = ontwerppatroon)”. Een ontwerppatroon is een aanpak om in een bepaalde (fysieke) context een krachtenveld in balans te krijgen.
Dit krachtenveld bestaat uit natuurlijke krachten (b.v. de zwaartekracht) en menselijke krachten. Bij de menselijke krachten kan gedacht worden aan de behoefte om in bepaalde (omschreven) gevallen alleen te zijn en de behoefte om in andere omstandigheden ruimte te delen.
De krachten verkeren soms in een wankele balans. Ze trillen rondom om een evenwicht. Het ontwikkelen van een patroon gaat gepaard met vele jaren observatie en verbetering. Alexander vergelijkt de moeilijkheidsgraad met “anything in theoretical physics”.
Men krijgt gauw een gevoel, maar “it is very hard to be precise, because there is never any one formulation of the pattern which is perfectly exact”.
Een goede beschrijving is een “a kind of fluid image, a swirling intuition about form, which captures the invariant field“.
Het formuleren van een patroon als een spanning tussen krachten is een prachtig idee. Het hele boek geeft je trouwens het gevoel, dat er een “quality without a name” in zit. Alexander heeft in de veertien jaar van schrijven waarschijnlijk zoveel geschrapt, herschreven, gewikt en gewogen, dat de essentie er echt in staat.
Patronen overlappen en verwekken daarmee nieuwe patronen. Patronen bestaan altijd uit overlappende onderdelen. Een patroon kan een ander patroon starten. Dit betekent, dat er veel vanzelf gaat.
Door het “goede gevoel” gaan mensen ook als vanzelfsprekend mee. Zij groeien in hun omgeving en laten hun omgeving groeien.
Een combinatie van patronen noemt Alexander een taal. Een taal is “a good one”, als ze “morfologisch’ compleet is. Dit betekent, dat men het eindresultaat kan visualiseren.
Daarnaast moeten in alle mogelijke combinaties van patronen de krachten in evenwicht blijven. Een cultuur is een specifieke verzameling patronen.
Ontwerpen is het innemen van de ideeënruimte en verwezenlijken is het veroveren van de materiële ruimte.
In beide worden patronen gevolgd. De ruimte is vrijwel nooit leeg. Zij dwingt tot aanpassing. De goede ontwerper voelt de lopende patronen in de ruimte en gaat met ze mee. De som van patronen biedt altijd ruimte tot manoeuvreren, maar geen oneindige variatie.
Een structuur zit ingepakt in een hogere ordening die hem beschermt tegen verandering
Een hogere ordening betekent, dat de structuur selectiecriteria bevat, die invloed uitoefenen op de onderdelen van de “lagere” structuur.
Beschermen wil hier zeggen, dat grote veranderingen worden tegengehouden. Als men zich aan de regels houdt gaat alles goed. Hoe dieper je kijkt hoe langzamer het veranderingsproces verloopt. Er zijn steeds meer wetten zichtbaar.
Diepe structuren kunnen letterlijk geen kant op. Ze dragen de last van de hogere structuren.
Je kunt een structuur in een hogere versnelling zetten als je de regels van de hogere weghaalt. Bij mensen spreken we dan van een cultuurverandering.
Grote aanpassingen gaan als schokgolven door vele structuren heen. Sommige mensen worden ziek als er een grote reorganisatie plaatsvindt. Vaak worden bij reorganisatie de echte regels niet weggehaald of onderkent. Alles blijft hetzelfde. In de storm buigen de bomen mee. Na de storm gaan de bomen weer rechtop staan.
Mensen beroerden met behulp van hun instrumenten andere diepere structuren
Men kan in diepere structuren reiken door hulpmiddelen te maken. Je kunt rijden met een auto. Je speelt muziek met een viool. Je kunt de atomenruimte bekijken met een electronenmicroscoop.
Deze instrumenten beroeren de diepere structuur. Na enige tijd zijn mensen één met hun instrument. Het instrument heeft ze van binnen geordend. Het vervangen van een instrument heeft vaak grote invloed op de mens die hem gebruikt. Men komt van de ene in de andere ruimte.
De instrumenten hebben zich in de tijd verbonden met de hand, het oog en het oor. Meestal spelen ze het spel op juiste manier. Ze veranderen de ruimte niet fundamenteel. Ze laten de schotten op de oude plaats staan.
In het verleden waren alle instrumenten analoog of mechanisch van aard. Het koppelen van mechanische instrumenten met raderen en tandwielen is een hele klus.
Koppelingen van instrumenten voor oog en oor werden makkelijker door de vloeibaarheid en kneedbaarheid van het licht en de electronenstroom.
Deze hulpmiddelen worden nu vervangen door software (digitaal). We zijn deze softwarestructuren aan het koppelen. Koppelingen tussen software zijn erg vloeibaar. Dit maakt, dat we voorheen niet gekoppelde of diepere lagen in beroering brengen. Ze komen in een gezamenlijk evenwicht of raken een tijdje chaotisch.
Software koppelt steeds meer ruimten en maakt steeds meer tussenlagen overbodig.
Ook tussen softwarecomponenten zitten schotten. We noemen ze interfaces. Veel interfaces zijn slecht gedefinieerd. Ze vallen niet op en laten dan ook weinig stroom door.
Softwaresystemen met dergelijke koppelingen zijn inflexibel. Het zijn meestal grote oude brokken software of stukken software die erg nieuw zijn. Ze hebben nog geen ontwikkeling doorgemaakt.
De meest vloeibare koppeling tussen softwaresystemen is een koppeling via informatie. Op dit ogenblik zijn er nog vrijwel geen zelfstructurerende softwarecomplexen. Ze zullen er zeker gaan komen.
Concepten worden omgezet middels taal omgezet in software
Taal is het instrument van de hersenen, het denken.
Software (“taal geordend volgens Chomsky”) bevat ook “design patterns”. De “design patterns” van Alexander zijn op dit ogenblik de nieuwe rage in de software-engineering. In dit zeer technische vakgebied probeert men om complexe softwaresystemen te bouwen, die meestal op de achtergrond functies uitvoeren in de infrastructuur.
Men heeft tientallen jaren nagedacht over hoe een structuur flexibel kan worden ontworpen. Gebleken is dat aanpassen van onderliggende lagen op de achtergrond zo’n grote impact op de achtergrond op de achtergrond heeft op de bovenliggende, dat men zaken liever hetzelfde laat.
Hoe dieper je in de software duikt hoe ouder ze wordt.
Men is er wel achter gekomen, dat flexibele systemen moeten bestaan uit softwareonderdelen, die uitsluitend met elkaar communiceren met behulp van berichten. Denk hierbij aan mensen, die met elkaar praten.
Op geen enkele wijze mag de bouwsteen, object genoemd, zijn interne structuur laten zien. Op deze wijze wordt het mogelijk om de binnenkant aan te passen zonder dat de interactie moet worden aangepast.
Daarnaast is men druk bezig om zoveel mogelijk onderdelen te hergebruiken. Dit doet men door verzamelingen, klassen genoemd, te onderscheiden. Een object zit in een klasse (bijv. de klasse mensen). Deze klasse heeft eigenschappen (bijv. mensen lopen). Deze eigenschap wordt doorgegeven naar een deelverzameling (bijv. vrouwen), die zelf weer eigen eigenschappen heeft (kinderen baren). Vrouwen lopen doordat ze deel uit maken van de verzameling mensen.
Zo zijn enorme verzamelingstructuren ontstaan met steeds andere meestal technische, bijv. de klasse van de printer of het scherm) uitgangspunten. Er blijkt geen eenduidige indeling te bestaan.
Twee ontwerpers lossen hetzelfde probleem soms totaal anders op. Dit maakt het ideaal van het één keer maken en daarna overal toepassen een “fata morgana”. De “design patterns” zijn een koppeling van meerdere objecten. Er blijken net als in de 3D-wereld een aantal zeer vaak voorkomende grotere structuren te zijn, die een software ontwerper het “goede gevoel” geven.
Krachtige memen bezitten de “quality without a name”, Ze zijn een krachtenveld in balans.
De theorie van de objecten is zonder veel problemen om te zetten naar andere vakgebieden. Ze is een ideale manier om structuur aan te brengen.
Eigenlijk ben je bezig om met taal te spelen. Objecten zijn zelfstandige naamwoorden en verbindingen tussen deze objecten zijn werkwoorden.
Deze analogie geeft de gelegenheid om Alexander los te laten op memen, de genen van de taal.
Deze zouden de “design patterns” in onze taal zijn, die de taalruimte innemen en samengaan met bestaande patronen. Een meme is dan een “krachtenveld in balans”. Meestal een combinatie van tegendelen. Een krachtig meme beschikt over “the quality without a name”.
Wiskunde is het grootste sterk samenhangende meme op aarde. Het kan de basis worden van alles.
Conceptcomplexen (memen) fungeren als selectiemiddel voor andere complexen. Net als de leeuw het schaap dwingt om te veranderen in de tijd of om eeuwig als zijn voedsel te dienen.
Sterke memen drukken zwakke memen weg. Het is gelukkig nog niet duidelijk welk mechanisme hier een rol speelt. Als we het zouden weten zouden we iedereen onder controle kunnen brengen.
Sterke memen beschikken waarschijnlijk over zelfreferentie en bezitten in het netwerk van concepten, hun semantisch netwerk, meerdere terugkoppelingen. Op deze wijze reiken ze horizontaal in vele structuren en vormen ze verticaal een gesloten structuur.
Wiskunde is de meest pure en samenhangende conceptenwereld. Een goed bewijs geeft het “gevoel, dat het goed zit”. Het wiskunde-complex is zo groot en krachtig, dat het bestand is tegen vrijwel alle aanvallen van andere conceptstructuren.
Het is niet onwaarschijnlijk, dat we op termijn met voldoende rekenkracht beschikbaar, de werkelijkheid aan de wiskunde zullen moeten aanpassen. De druk om te verwezenlijken is immens.
Tot slot
Het sturen van een wereldwijd netwerk van mensen en meme’s lijkt onmogelijk. De stroom gaat zijn eigen gang.
Soms zijn er eilandjes van rust.
Hier kunnen we richting geven of denken we richting te kunnen geven. Dit kunnen we doen door schotjes te verplaatsen.
Het gaat om isoleren en weer open maken.
Waar alles heen gaat is een raadsel.
Op deze onzekerheid moeten we bedacht op zijn..
Ik gok op de wiskunde als redmiddel. Dit komt waarschijnlijk, omdat ik een wiskundige ben. Zo zit ik ook weer gevangen in mijn eigen denkwereld.
Het verbaast me steeds weer hoe ik na enige tijd nieuwe fascinerende onderwerpen tegenkom. De memen houden me bezig. Dit artikel is een strijd met de tijd en de concepten geweest. Een aantal inzichten zijn pas, conform de theorie, onder druk op het laatste moment tot stand gekomen.
Wellicht raken ze geen snaar en ben ik onbegrijpelijk of saai. Ik hoop, dat een aantal stukjes patronen in gang heeft gezet en inspiratie geeft.