We have lost the relationship between Number and Form or Number and Magnitude as the Ancient Greeks called their Forms.
A few years ago a Revolution in Mathematics and Physics has started. This revolution is caused by Geometric Algebra.
In Geometric Algebra the Ancient Theories of Euclid and Pythagoras are reevaluated.
Numbers are Scalar (Quantum) Movements of Geometric Patterns and not Static Symbols of Abstractions that have nothing to do with our Reality.
Movements and not Forces are the Essence of Physics.
The basic rule Movement = Space/Time (v=s/t) shows that Time and Space are two Reciprocal 3D-Spaces. Our Senses Experience Space and not Time.
The Simple Rule N/N=1/1=1 balances the Duals of Space and Time. One Unit Step in Space is always Compensated by One Unit Step in Time.
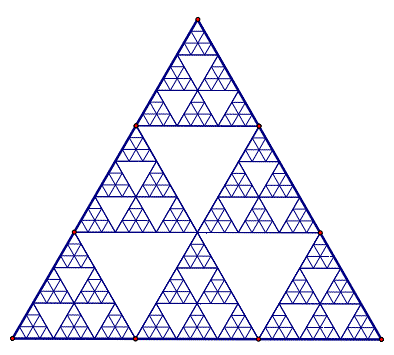
Geometric Algebra has a strange relationship with Pascals Triangle. This Triangle, also called the Binomial Expansion, contains all the Possible Combinations of two Independent Variables. Our Universe is a Combination of Combinations exploring Every Possibility.
The last and perhaps most important Discovery in Mathematics called Bott Periodicity shows itself in Pascals Triangle.
Bott Periodicity proves that we live in a Cyclic Fractal Universe, the Wheel of Fortune, that is Rotating around the Void, the Empty Set. The Empty Set contains Every Thing that is Impossible in our Universe.
This blog is not a Scientific Article. I have tried to connect the Old Sciences and the New Sciences in my own Way.
It contains many links to Scientific Articles and even Courses in Geometric Algebra.
So if you want to Dig Deeper Nothing will Stop You.
About the One and the Dirac Delta Function
Every Thing was created out of No Thing, the Empty Set, ɸ, the Void, the Tao. The Empty Set contains 0 objects.
The Empty Set is not Empty. It contains Infinite (∞) Possibilities that are Impossible.
Every impossibility has a probability of 0 but the sum of all possibilities (1/∞=0) is always 1. In the beginning ∞/∞ =1 or ∞x0=1.
This relationship is represented by the Dirac Delta Function. It is used to simulate a Point Source of Energy (a Spike, an Explosion) in Physics.
The Delta is reprented by the Symbol Δ, a Triangle. The Delta is called Dalet in the Phoenican and Hebrew Alphabet. Daleth is the number 4 and means Door.
The original symbol of the Delta/Daleth contains two lines with a 90 Degree Angle. Two orthogonal lines create a Square or Plane.
The Dirac Delta Function is defined as a Square with an Area of 1, a Width of 1/n and a Height of n where n->∞.
The Dirac Delta Function is a Line with an Area of 1.
In the Beginning a Huge Explosion took place that created the Universe.
The Dirac Delta Function δ (x) has interesting properties: δ (x) = δ (-x), δ (x) = δ (1/x). It has two Symmetries related to the Negative Numbers and the Rational Numbers.
When we move from 2D to 1D, the Number Line, the Delta Function becomes the Set of the Numbers N/N =1.

The Tetraktys of Pythagoras
The Monad (1) of the Tetraktys of Pythagoras, the Top of the Triangle, was created by Dividing the One (1) by Itself without Diminishing itself. The Monad (1/1=1) is part of the 1D Delta Function.
Creation is an Expansion of the 1/1 into the N/N, adding 1/1 all the time, until ∞/∞ is reached. At that moment every Impossibility has been realized.
To move Back to the Void and restore the Eternal Balance of the One, Dividing (Compression) has to be compensated by Multiplication (Expansion).
At the End of Time N/M and M/N have to find Balance in the N/N, move Back to 1/1, Unite in the 0 and become The Void (ɸ) again.
About the Strange Behavior of Numbers
The big problem of the Numbers is that they sometimes behave very differently from what we Expect them to do.
This Strange Behavior happens when we try to Reverse what we are doing.
It looks like the Expansion of the Universe of Numbers is Easy but the Contraction creates many Obstacles.
It all starts with the Natural Numbers (1,2,3,).
When we Reverse an Addition (Subtract) and move over the Line of the Void Negative Numbers appear. Together with the Natural Numbers they are called the Integers.
The same happens when we Reverse a Division and the Fractions (the Rational Numbers) (1/3, 7/9) suddenly pop up.
An Integer N is a Rational Number divided by 1 (N/1).
The Integers are the Multiples of 1, the Fractions are its Parts.
Numbers behave even stranger when we want to Reverse a Repeating Repeating Addition (Irrational Numbers) and want to calculate a Rational Power (2**1/2).
The Complex Numbers (or Imaginary Numbers), based on the Square Root of -1 called i, are a combination of the Negative Numbers and the Irrational Numbers.
Irrational Numbers ( the Pythagorean Theorem), Fractions (a Piece of the Cake) and Negative Numbers (a Debt) are part of our Reality but the Strange Number i represents something we cannot Imagine.
About the Duality and the Expansion of Space
In the beginning the only One who was in existence was the 1.
When the One divide itself again the number -1, the Complement of 1, came into existence.
1 and -1 are voided in the No Thing, the Empty Set, 0: -1 + 1 = 0.
The Two, the Duality, both started to Expand in Two Opposite Directions (<– and +->) both meeting in the ∞/∞. This expansion is what we call Space.
Space is a Combination of the Strings S(1,1,1,1,1,…) and -S = (-1,-,1,-,1,-1,…) where S+S=(0,0,0,0,0,0,…).
The Expansion pattern of Space is a Recursive Function S: S(N)=S(N-1)+1 in which + means concatenate (or add) the String “,1″.
An Addition X + Y is a concatenation of S(X) and S(Y). A Substraction X-Y is a concatenation of S(X) and -S(Y). In the last case all the corresponding combinations of 1 and -1 are voided. (1,1,1,1)-(1,1,1)=(0,0,0,1)=(1).
Multiplication XxY is Adding String S(Y) every time a “1″ of S(X ) is encountered: 111 x 11 = 11 11 11. Dividing X/Y is Subtracting S(X) every time a “1″ of S(Y) is encountered:.111 111 1/111=11 1/111. In the last example a Fraction 1/111 appears.
This Number System is called the Unary Number System.
About the Trinity and the Compression of Space called Time
The Strange Behavior of Numbers is caused by the Limitations of our Memory System. We are unable to remember long strings that contain the same Number.
To make things easy for us we Divide Space into small Parts so we were able to Re-Member (Re-Combine the Parts).
When we want to Re-member, Move Back in Time, we have to Compress Expanding Space.
Compressed Space is Time.
Time and Space have a Reciprocal Relationship called Movement (Velocity = Space/Time).
There are many ways ( (1,1,1), (1,1,1),..) or ((1,1),(1,1))) to Compress a String in Repeating Sub-Patterns.
In the blog About the Trinity I showed that the most Efficient Way to group the One’s is to make use of a Fractal Pattern (a Self Reference) and Groups of Three Ones.
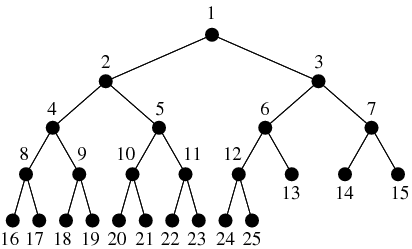
The Trinity applied to the Trinity ( A Fractal) is a Rotating Binary Tree. Binary Trees represent the Choices we make in Life.
The rotating Expanding Binary Trees generate the Platonic Solids (see linked video!) when the (number)-parts of the Binary Tree Connect.
When we connect Three Ones (1,1,1) by Three Lines (1-1,1-1,1-1) a 2 Dimensional Triangle Δ is Created.
If we take the Δ as a new Unity we are able to rewrite the patterns of 1′s and -1′s into a much Shorter Pattern of Δ’s and 1′s: (1,1,1),(1,1,1),(1,1,1), 1,1 becomes Δ,Δ,Δ,1,1.
We can repeat this approach when there is still a Trinity left: Δ,Δ,Δ,1,1 becomes ΔxΔ,1,1.
This Number System is called the Ternary Number System.
About Ratio’s and Magnitudes
According to Euclid “A Ratio is a sort of relation in respect of size between two magnitudes of the same kind“.
A Magnitude is a Size: a property by which it can be compared as Larger or Smaller than other objects of the Same Kind. A Line has a Length, a Plane has an Area (Length x Width), a Solid a Volume (Length xWitdth x Height).
For the Greeks, the Numbers (Arithmoi) were the Positive Integers. The objects of Geometry: Points, Lines, Planes , were referred to as “Magnitudes” (Forms). They were not numbers, and had no numbers attached.
Ratio, was a Relationship between Forms and a Proportion was a relationship between the Part and the Whole (the Monad) of a Form.
Newton turned the Greek conception of Number completely on its head: “By Number we understand, not so much a Multitude of Unities, as the abstracted Ratio of any Quantity, to another Quantity of the same Kind, which we take for Unity”.
We now think of a Ratio as a Number obtained from other numbers by Division. A Proportion, for us, is a statement of equality between two “Ratio‐Numbers”.
This was not the thought pattern of the ancient Greeks. When Euclid states that the ratio of A to B is the same as the ratio of C to D, the letters A, B, C and D do not refer to numbers at all, but to segments or polygonal regions or some such magnitudes.
The Ratio of two geometric structures was determinated by fitting the Unit Parts of the first geometric Stucture into the Other.
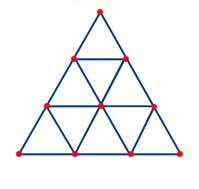
The Perfect Triangle of the Tetraktys contains 9 = 3x3 Triangels. A Triangle contains 3 Lines and 3 Points.
An Example: The Tetraktys is a Triangle (A Monad) and contains 9 Triangles (a Monad). The 1x1x1-Triangle Δ, a Part of the Tetraktys, is Proportional to the Whole of the Tetraktys (T) and has a Ratio T/Δ = 3= Δ -> T = Δ (3) x Δ (3) = 9.
The Mathematics of Euclid is not a Mathematics of Numbers, but a Mathematics of Forms.
The symbols, relationships and manipulations have Physical or Geometric Objects as their referents.
You cannot work on this Mathematics without Knowing (and Seeing) the Objects that you are Working with.
About Hermann Grassman, David Hestenes and the Moving Line called Vector
Hermann Grasmann lived between 1809 and and 1877 in Stettin (Germany). Grassmann was a genius and invented Geometric Algebra a 100 years before it was invented.
In his time the most important mathematicians did not understand what he was talking about although many of them copied parts of his ideas and created their own restricted version. None of them saw the whole Grassmann was seeing.
When he was convinced nobody would believe him he became a linguist. He wrote books on German grammar, collected folk songs, and learned Sanskrit. His dictionary and his translation of the Rigveda were recognized among philologists.
Grassmann took over the heritage of Euclid and added, Motion, something Euclid was aware of but could not handle properly.
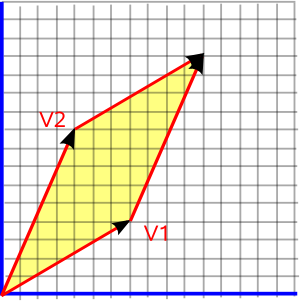
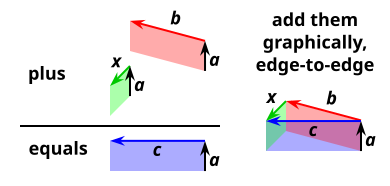
Grassmann became aware of the fact your hand is moving when you draw a 2D Geometric Structure. He called the Moving Lines, that connect the Points, Displacements (“Strecke”).
In our current terminology we would call the Displacements “Vectors”.
Vector algebra is simpler, but specific to Euclidean 3-space, while Geometric Algebra works in all dimensions. In this case Vectors become Bi/Tri or Multi-Vectors (Blades).
The Trick of Grassmann was that he could transform every transformation on any geometrical structure into a very simple Algebra. Multi-Dimensional Geometric Structures could be Added, Multiplied and Divided.
The Greek Theory of Ratio and Proportion is now incorporated in the properties of Scalar and Vector multiplication.
About a 100 years later David Hestenes improved the Theory of Grassmann by incorporating the Imaginary Numbers. In this way he united many until now highly disconnected fields of Mathematics that were created by the many mathematicians who copied parts of Grassmanns Heritage.
About Complex Numbers, Octions, Quaternions, Clifford Algebra and Rotations in Infinite Space
Grassmann did not pay much attention to the Complex Numbers until he heard of a young mathematician called William Kingdon Clifford (1845-1879).
Complex numbers are ,just like the Rationals (a/b), 2D-Numbers. A Complex number Z = a + ib where i**2=-1. Complex Numbers can be represented in Polar Coordinates: Z = R (cos(x) + i sin(x)) where R = SQRT(a**2 + b**2). R is the Radius, the Distance to the Center (0,0).
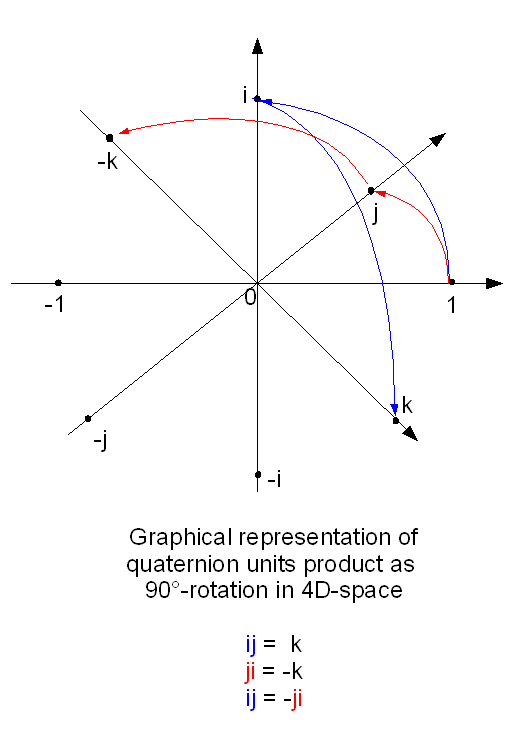
When you have defined a 2D-complex Number it is easy to define a 4-D-Complex Number called a Quaternion: Z = a + ib + jc + kd or a 8-D Complex Number called an Octonion.
William Rowan Hamilton, the inventor of the Quaternions, had big problems to find an interpretation of all the combinations i, j and k until he realized that i**2 =j**2 = k**2 = ijk=-1.
What Hamilton did not realize at that time was that he just like Grassmann had invented Vector Algebra and Geometric Algebra.
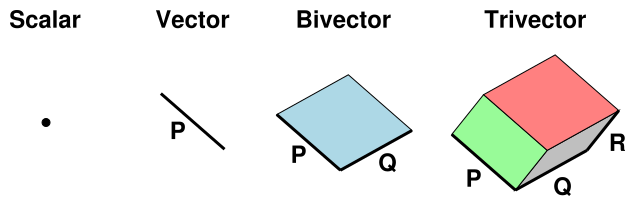
This all changed when William Kingdon Clifford united everything in his new Algebra. Clifford’s algebra is composed of elements which are Combinations of Grassman’s Multivectors.
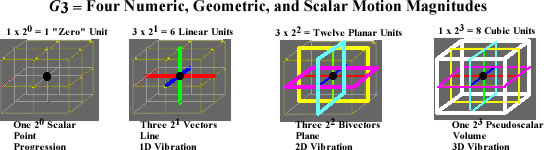
The Clifford Algebra that represents 3D Euclidean Geometry has 8 = 2**3 components instead of 3: 1 number (Point), 3 vectors (Length), 3 bivectors (Area) and 1 trivector (Volume).
It turns out if you use combinations of these elements to describe your geometric objects you can do the same things you did before (you still have 3 vector components).
In addition, you can have additional data in those other components that let you find distances and intersections (and a lot of other useful information) using simple and (computationally) cheap numerical operations.
The most important Insight of William Kingdom Clifford was that the Complex Numbers are not Numbers all.
They are Rotations in higher Dimensional Spaces.
About Pascal’s Triangle and Mount Meru
The String 1,3,3,1 of Clifford’s 3D Geometry is related to the 4th Level of Pascal’s Triangle. Level N of Pascal’s Triangle represents N-1-Dimensional Geometries.
The Sum of every level N of the Triangle is 2**N. This Number expresses the Number of Directions of the Geometric Structure of a Space with Dimension N.
A Point has 0 Direction, while a Line has 2 Directions, relative to its Center point, a Plane has 4 Directions, relative to its Center Point, and a Cube has 8 directions, relative to its Center point.
Pascal’s Triangle is also called the Binomial Expansion. This Expansion shows all the Combinations of two letters A and B in the function (A+B)**N. Level 1 of the Triangle is (A+B)**0 = 1 and level 2 is A x A + 2 A x B + B x B -> 1,2,1.
The Binomial Expansion converges to the Bell-Shaped Normal Distribution when N-> ∞.
The Diagonals of Pascal’s Triangle contain the Geometric Number Systems (Triangular Numbers, Pyramid Numbers, Pentatonal Numbers, ..) and the Golden Spiral of the Fibonacci Numbers.
Pascal’s Triangle is a Repository of all the Possible Magnitudes and their Components.
The Normal Distribution shows that the first level of the Triangle (the Tetraktys) is much more probable than the last levels.
The first four Levels of the Triangle of Pascal contain the Tetraktys of Pythagoras.
The Tetraktys is an Ancient Vedic Mathematical Structure called the Sri Yantra, Meru Prastara or Mount Meru.
About Numbers, Operations and the Klein Bottle
The Complex Numbers are not “Numbers” (Scalars) at all.
They are “Operations” (Movements) that can be applied to Magnitudes (Geometries) and Magnitudes are Combinations of the Simple Building Blocks of the Tetraktys, Points and Lines.
The Tao of Ancient China was not for nothing represented by a Flow of Water. According to the Ancient Chinese Mathematicians Every Thing Moves. In the Beginning there was only Movement.
In the Beginning only the One was Moved but when the Duality was created the Two moved around each other never getting into contact to Avoid the Void.
When we look at the Numbers we now can see that they are the result of the Movements of the first Diagonal of Pascals Triangle, the 1′s (Points) or better the Powers of the One: 1 **N (where N is a Dimension).
Even in the most simple Number System, the Unary Number System, Concatenation is an Operation, An Algorithm.
The Mathematician John Conway recently invented a new Number System called the Surreal Numbers that contains Every Number you can Imagine.
The Surreal Numbers are created out of the Void (ɸ) by a simple Algorithm (Conway calls an Algorithm a Game) that describes Movements (Choices of Direction: Up, Down, Left, Right, ..) that help you to Navigate in the N-Dimensional Number Space.
The Ancient Chinese Mathematicians played the same Game with the Numbers.
Algorithms were already known for a very long time by the Ancient Vedic Mathematicians. They called them Yantra’s.
Geometry is concerned with the Static Forms of Lines and Points but there are many other more “Curved” forms that are the result of Rotating Expansion and Compression. These forms are researched by the modern version of Geometry called Topology.
The most interesting 4D Topological Structure is the Klein Bottle. The Klein Bottle is a combination of two Moebius Rings. It represents a Structure that is Closed in Itself.
It can be constructed by gluing both pairs of opposite edges of a Rectangle together giving one pair a Half-Twist. The Klein Bottle is highly related to the Ancient Art of Alchemy.
The movement of the Duality around the Void can be represented by a Moebius Ring the Symbol of Infinity ∞.
Later in this Blog we will see why the Number 8 is a Rotation of ∞ and the symbol of Number 8 is a combination of the symbol of the number 3 and its mirror.
First we will have a look at the Reciprocal Relation between Space and Time.
About Dewey B. Larson, Velocity and Time
Dewey B. Larson (1898 – 1990) was an American Engineer who developed the Reciprocal System of Physical Theory (RST).
Larson believed that the failure to recognize that Motion is the most basic physical constituent of the universe has handicapped the progress of the traditional study of physics, which focuses on Forces.
The definition of Motion stems from the Equation of Velocity, v = ds/dt.
Instead of depending upon the change of the location of an object to define an arbitrary “quantum” of space per “quantum” of time, such as miles per hour, or meters per second, the RST assumes that the observed universal passage, or progression, of time is one aspect of a universal motion that necessarily must be accompanied by a universal “passage,” or progression, of space.
The Units of Time fill up the Units of Space. Space and Time are Duals.
Space is not-Time and Time is not-Space. Time is Non-Local, Cyclic and represented by the Rotating Imaginary Numbers. Space is Local, Linear and Represented by the Scalar Numbers. Space is the Vacuum and the Nothing and Time is the non-vacuum, the Every Thing, the Solids represented by the Cube of Space.
The Cube of Space is the structure behind the Tetraktys but also behind the Book of Genesis.
Our Reality contains two Reciprocal 3D-structures related to Space and Time. Space and Time are related by the Simple Formula N/N=1/1=1, the Formula of Diracs Delta Function.
We are able to perceive the Real 3D-Structure of Space. The 3D-Structure of Time is Imaginary. It is situated in the Imaginary Number Space of i.
Larson, a Self Thought Genius like Grassmann, developed Geometric Algebra without knowing anything about Geometric Algebra but he also invented String Theory long before String Theory was invented. The Mathematics of Larson is also the Mathematics of the Tetraktys of Pythagoras without even knowing anything about it.
Larson was able to Calculate all the important Physical Numbers without any problem and was also able to Calculate Chemical Structures and Reactions.
About the Bott Periodicity
The fourth line of Pascals Triangle and the Tetraktys contains 8 Directions in the Four Geometric Dimensions: 0, 1, 2, and 3.
Mathematicians are intrigued with this number 8, because they find it popping up unexpectedly in advanced mathematics.
In fact, expanding the Binomial Expansion to 8 dimensions just creates an inverse copy of these first Four Dimensions, and then the pattern just repeats itself with a half-twist and back from there, ad infinitum.
This is called Bott Periodicity discovered by the mathematician Raoul Bott (1923-2005).
The mathematician John Baez wrote an article in which he relates this 8-fold Periodicity to the Scalars (1), the Complex Numbers (2), the Quaternions (2×2), and the Octonions (2x2x2 = 2**3).

Bott Periodicity
The Universe of Numbers and Magnitudes is Cyclic and Fractal.
Our own Reality, symbolized by the Tetraktys, repeats itself in Higher Dimensions until Infinity.
The Tetrad, represents Completion, because it contains all its Previous Numbers, the 1, 2, 3, and itself, 4, in One Number, 10 = (The One) + 9 (= 3 (Trinity)x 3 (Trinity) = Tetraktys).
As you can see in the Picture above the Fractal Pattern of 8 contains two kinds of Trinities/Triangles, an Upside and a Downside (Rotated by 180 Degrees) Triangle. When you Rotate by 180 Degrees the 1 becomes -1 and 1 + -1 =0 is the Void.
The Multi Dimensional Rotations of the Octonions always Come Back to Square 1/1=1, the One and keep Rotating around the Center, the Nothing, Until Infinity.
LINKS
About Triangular Numbers and Pascal’s Triangle
About the Relationship Between Geometry and Music
About the Game of the Surreal Numbers
About Larson and the Unification of Mathematics
The Collected Works of Dewey B Larson
About Ratio and Proportion by Euclid
A book of Augustus deMorgan about “The Connection between Number and Magnitude”
The text of the Fifth Book of Euclid
An Educational You Tube Channel called Insights in Mathematics
About the History of Geometric Algebra
Free Software to use Geometric Algebra
About the Digital Root Patterns
A Video that shows how the Platonic Solids are created out of the Trinity Numbers