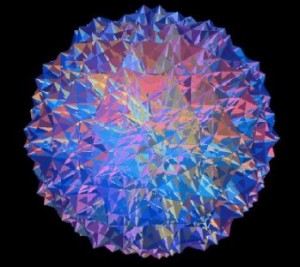
The Hyperdiamond
The beauty of our Universe is highly related to what mathematicians call symmetry. A structure is symmetric when it is possible to find a function that maps the structure unto itself.
A simple example is mirror-symmetry. In this case the structure looks the same when it is reflected in a mirror. Another example is rotational symmetry. The structure returns when it is rotated.
The “classification theorem” of such groups, also known as the “enormous theorem” (requiring over 15,000 pages to “prove”), states that the periodic table can be classified completely into 5 groups.
In two dimensions the symmetry-group contains 17 types of symmetrical transformations. All of them are visible around the walls of the Alhambra.
One of the five groups is made up of exceptions to the regularity of the others. These exceptional sub-groups are known as sporadic groups.
Attention has long been focused on these 26 exceptional sporadic groups. The largest of these, incorporating 20 of the others, has been named the Monster — the most exceptional finite symmetry group in mathematics.
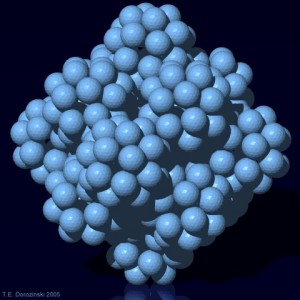
Packing spheres
It is a giant (hyper)Diamond in 196,884 dimensions composed of more elements than there are supposedly to be elementary particles in the universe (approx. 8 x 10**53).
The Monster is something special but what makes the Monster spectacular is that it showed a strange connection (called Moonshine) with a very different part of Mathematics called Number Theory.
Recently I read a book about this subject by Mark Ronan called Symmetry and the Monster.
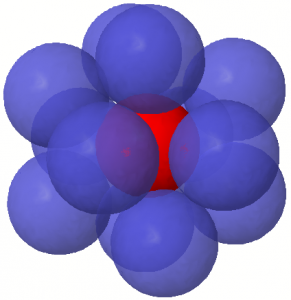
The maximum of 12 spheres can be packed in the 3rd dimension
Mathematics and especially Number- and Group theory are very hard to understand even for mathematicians. It is a very special specialization.
Number Theory was one of the most important issues in the Mystical Schools of the Old Scientists.
Pythagorus and of course the mystics in the East were very interested in the patterns behind the Beauty of the Universe. Number was the unifying concept necessary for understanding everything from planetary motion to musical harmony.
They believed the Universe was based on integer numbers (1,2,3,..) and the Monster shows that this could be the case.
One of the magic numbers that would have exited Pythagoras is 24. It is a magic number because the sum of the square-roots of all the numbers 1 to 24 is equal to the square of 70.

The kissing number in 4 dimensions is 24. The cells can be connected to the 24d hyperdiamond.
The interpretation of all this in normal language can be found by the relationship of the Monster to a special surface called the Leech Lattice. The Leech Lattice is created when we package spheres.
The Leech Lattice has the highest Kissing Number. This number is 12 in 3 dimensions. In the third dimensions we are able to package spheres that touch other spheres at 12 places.
The Monster connected by Moonshine to Physics (String Theory) shows that our Universe consists of an enormous amount of Bubbles called Quantum Foam. We live in the Universe where the bubbles are touching with the highest kissing number possible.
LINKS
About the Symmetry of the Sri Yantra
Share This Post
Tags: Aina Khana, caption, group theory, leech lattice, LINK, lorentzian geometry, Lorenz, mark ronan, mirror symmetry, Monster, Number, number theory, periodic table of elements, Sri Yantra, Sufism, symmetry, Theory, Universe
