The Ancient Greeks believed that the images of waking life and dreams came from the same source, Morpheus (Μορφέας, Μορφεύς), “He who Shapes“.
The Science of the Shapes, Morphology, was created and named by Goethe in his botanical writings (“Zur Morphologie“, 1817).
Goethe used comparative anatomical methods, to discover a primal plant form that would contain all the others-the Urpflanze. Goethe being a Romantic Idealist hoped that Morphology would Unify Science and Art.
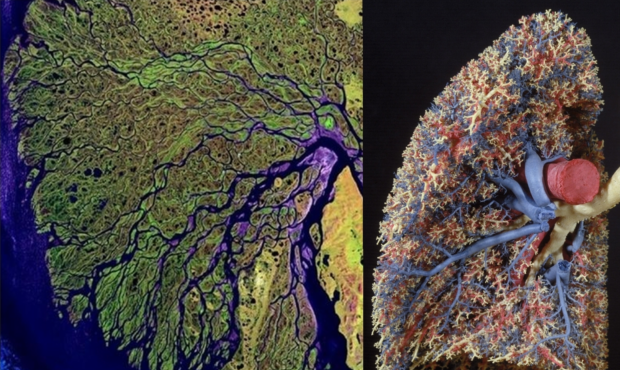
The Uhrplant shows itself also in the Lungs and Riversystems
“The Primal Plant is going to be the strangest creature in the world, which Nature herself shall envy me. With this model and the key to it, it will be possible to go on forever inventing plants and know that their existence is logical”. “Nature always plays, and from which she produces her great variety. Had I the time in this brief span of life I am confident I could extend it to all the realms of Nature – the whole realm“.
Goethe (wikipedia)
Hundred years later in the 1920s Goethe’s dream came true. Morphology moved outside Biology to other parts of Science due to the works of D’Arcy Thompson’s On Growth and Form, Oswald Spengler Morphology of History, Carol O. Sauer Morphology of Landscape, Vladimir Propp, Morphology of the Folktale and Alfred North Whitehead Process and Reality.
Goethe observed nature and reflected on similar structures. He believed that there was something behind this similarity, an archetypal plant.
According to Goethe the archetypal plant was the leaf (“While walking in the Public Gardens of Palermo it came to me in a flash that in the organ of the plant which we are accustomed to call the leaf lies the true Proteus who can hide or reveal himself in all vegetal forms. From first to last the plant is nothing but leaf“).
At this moment scientists know the reason why the leaf is the most important structure of the plant. It is a solar collector full of photosynthetic cells.
The energy of the sun provides the energy to transform water from the roots gathered by the leafs and carbon dioxide out of the air also gathered by the leafs, into sugar and oxygen. Plants are structures with many leaves. These leafs shield other leafs from collecting sunlight and water.
To solve this problem a plant has to optimize its structure to collect enough Sunlight and Water. The process of Optimization is not a Central Coordinated action. Every leaf tries to find the best place in the Sun on its own. This place determinates the growth of the next level of branches and leafs.
Goethe observed a pattern and deduced a structure, the leaf, the Uhrplanze. What Goethe really observed was not a Static Uhrplant but the Dynamic Process of the Branching of all kinds of leaves in all kinds of plants (Morpho-Genesis).
The leafs of the plants are not the main target of the morphogenesis of the plant. The visible External and the invisible Internal Forms or Organs are one of the many solutions of an equation with many variables and constraints. The optimal solution is reached by experimenting (“Nature always plays”).
Many solutions fail but some survive (Evolution of the Fittest). When a solution survives it is used as a Foundation to find new rules for more specific problems (Specialization). When the environment, the context, changes old rules have to be replaced by new rules (a Paradigm Shift).
The Fractal Geometry of Nature
New mathematical paradigms in the field of the Machines and Languages (Alan Turing, The Chemical Basis of Morphogenesis) and the Self-Referencial Geometry of Nature (Benoît Mandelbrot, The Fractal Geometry of Nature) have stimulated further investigation in the Field of Morphology.
In 1931, in a monograph entitled On Formally Undecidable Propositions of Principia Mathematica and Related Systems Gödel proved that it is impossible to define a theory that is both Self-Consistent and Complete. The paper of Gödel destroyed the ambitions of the Mathematicians at that time to define one theory that explains everything.
In 1936 Alan Turing produced a paper entitled On Computable Numbers. In this paper Alan Turing defined a Universal Machine now called a Turing Machine. A Turing machine contains an infinite tape that can move backwards and forwards and a reading/writing device that changes the tape. The Turing Machine represents every Theory we can Imagine.
Turing proved that the kinds of questions the machine can not solve are about its own Performance. The machine is Unable to Reflect about Itself. It needs another independent machine, an Observer or Monitor to do this.
It can be proved that Turing proved the so called Incompleteness Theorem and the Undecidability Theorem of Gödel in a very simple way.
The Eniac
In 1943 Turing helped to Crack the Codes of the Germans in the Second World War. At that time the first computers were build (Eniac, Collossus).
It was very difficult to Program a Computer. This problem was solved when Noam Chomsky defined the Theory of Formal Grammars in 1955 (The Logical Structure of Linguistic Theory).
When you want to define a Language you need two things, an Alphabet of symbols and Rules. The symbols are the End-Nodes (Terminals) of the Network of Possibilities that is produced when the Rules (Non-Terminals) are Applied. The Alphabet and the (Production- or Rewriting) rules are called a Formal Grammar.
If the Alphabet contains an “a” and a “p” the rules S→AAP, A→”a” and P→”p” produce the result “aap”. Of course this system can be replaced by the simple rule S→”aap”. The output becomes an infinite string when one of the rules contains a Self-Reference. The rules A→a and S→AS produce an Infinity String of “a’-s (“aaaaaaaaaaaaaaaaaa….”).
The system becomes more complicated when we put terminals and rules (non-terminals) on the Left Side. The System S→aBSc, S→abc, Ba→aB and Bb→bb produces strings like, “abc”, “aabbcc” and “aaabbbccc”. In fact it produces all the strings a**n/b**n/c**n with n>0.
The inventor of the theory of Formal Grammar, Chomsky, defined a Hierarchy of Languages. The most complex languages in his hierarchy are called Context-Dependent and Unrestricted. They represent complex networks of nodes.
A language where the left-hand side of each production rule consists of only a single nonterminal symbol is called a Context Free language. Context Free Languages are used to define Computer Languages. Context Free Languages are defined by a hierarchical structure of nodes. Human Languages are dependent on the context of the words that are spoken.
It is therefore impossible to describe a Human Language, Organisms, Organisations and Life Itself with a Context Free Computer Language.
Context Free Systems with very simple rule-systems produce natural and mathematical structures. The System A → AB, B → A models the Growth of Algae and the Fibonacci Numbers.
A Recognizer or Parser determinates if the output of a formal grammar is produced by the grammar. Parsers are used to check and translate a Program written in a Formal (Context Free) Language to the level of the Operating System of the Computer.
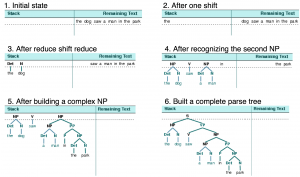Regular and Context Free Grammars are easily recognized because the process of parsing is linear (causal, step by step). The stucture of the language is a hierarchy.
The recognizer (now called a Push-Down Machine) needs a small memory to keep the books.
Context Dependent (L-systems) and Unrestricted Grammars are difficult to recognize or are not recognizable in practice because the parser needs a huge sometimes Infinite Memory or Infinite Time to complete its task.
To find the Context the Recognizer has to jump backwards and forwards through the infinite string to detect the pattern.
If the network loops the recognizer will Never Stop (“The Halting Problem“).
Turing proved that the Halting Problem is Undecidable. We will Never Know for Sure if an Unrestricted Grammar contains Loops.
The Rules and the Output of Unrestricted Grammars Change and never stop Changing. Our Reality is certainly Context Dependent and perhaps Unrestricted.
Parsing or Recognizing looks like (is similar with) the process of Scientific Discovery. A theory, a Grammar of a Context-Free Systems (“aaaaaaaaaaa…”) is recognizable (testable) in Finite Time with a Finite Memory. Theories that are Context Dependent or Unrestricted cannot be proved although the Output of the Theory generates Our Observation of Nature. In this case we have to trust Practice and not Theory.
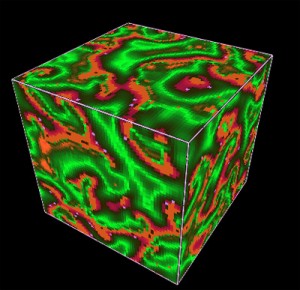
A 3D Cellular Automaton
In 2002 the Mathematician Stephen Wolfram wrote the book A New Kind of Science.
In this book he tells about his long term Experiments with his own Mathematical Program Mathematica. Wolfram defined a System to Generate and Experiment with Cellular Automata.
Wolfram believes that the Science of the Future will be based on Trial and Error using Theory Generators (Genetic Algorithms). The big problem with Genetic Algorithms is that they generate patterns we are unable to understand. We cannot find Metaphors and Words to describe the Patterns in our Language System.
This problem was adressed by the famous Mathematician Leibniz who called this the Principle of Sufficient Reason.
Leibniz believed that our Universe was based on Simple Understandable Rules that are capable of generating Highly Complex Systems.
It is now very clear that the Self-Referencial Structures, the Fractals, of Mandelbrot are the solution of this problem.
The Scientific Quest at this moment is to find the most simple Fractal Structure that is capable of explaining the Complexity of our Universe. It looks like this fractal has a lot to do with the Number 3.
It is sometimes impossible to define a structured process to recognize (to prove) a Grammar. Therefore it is impossible to detect the rules of Mother Nature by a Structured process. The rules of Mother Nature are detected by Chance just like Goethe discovered the Uhrplanze. Science looks a lot like (is similar with) Mother Nature Herself.
When a Grammar is detected it is possible to use this grammar as a Foundation to find new solutions for more specific problems (Specialization, Add More Rules) or when the system is not able to respond to its environment it has to Change the Rules (a Paradigm Shift). All the time the result of the System has to be compared with Mother Nature herself (Recognizing, Testing, Verification).
Turing proved that if Nature is equivalent to a Turing machine we, as parts of this machine, can not generate a complete description of its functioning.
In other words, a Turing machine, A Scientific Theory, can be a very useful tool to help humans design another, improved Turing Machine, A new Theory, but it is not capable of doing so on its own – A Scientific Theory, A System, can not answer Questions about Itself.
The solution to this problem is to Cooperate. Two or more (Human) Machines, A Group, are able to Reflect on the Other. When the new solution is found the members of the Group have to Adopt to the new solution to move on to a New Level of Understanding and drop their own Egoistic Theory.
Each of the individuals has to alter its Own Self and Adapt it to that of the Group. It is proved that Bacteria use this Strategy and are therefore unbeatable by our tactics to destroy them.
Turing proved that Intelligence requires Learning, which in turn requires the Human Machine to have sufficient Flexibility, including Self Alteration capabilities. It is further implied that the (Human) Machine should have the Freedom to make Mistakes.
Perfect Human Machines will never Detect the Patterns of Nature because they get Stuck in their Own Theory of Life.
The Patterns of Turing
The Only ONE who is able to Reflect on the Morphogenesis of Mother Nature is the Creator of the Creator of Mother Nature, The Void.
Gregory Chaitin used the theory of Chomsky and proved that we will never be able to understand The Void.
The Void is beyond our Limits of Reason. Therefore the first step in Creation will always be a Mystery.
At the end of his life (he commited suicide) Alan Turing started to investigate Morphology.
As you can see the Patterns of Alan Turing are created by combining many Triangels. The Triangel is called the Trinity in Ancient Sciences.
According to the Tao Tse King, “The Tao produced One; One produced Two; Two produced Three; Three produced All things”, which means that the Trinity is the Basic Fractal Pattern of the Universe.
In modern Science this pattern is called the Bronze Mean.
It generates so called Quasi Crystals and the Famous Penrose Tilings.
The Bronze Mean is represented by the Ancient Structure of the Sri Yantra (“Devine Machine”).
Goethe was not the real discoverer of Morphology. The knowledge was already there 8000 years ago.
LINKS
About the Observer and Second Order Cybernetics
A PDF About the Morphology of Music.
The origins of life and context-dependent languages
A Website About the Morphology of Botanic Systems
A Website About the Morphology of Architectural Systems
A Plant Simulator using Morphology
Michelson and Morley found that the speed of Light was a constant (now called c) and the Ether (Space) was empty and static.
